142 Enem 2020 – Três amigos, André, Bernardo e Carlos, moram em um condomínio fechado de uma cidade…

142 PROVA AMARELA ENEM 2020)

Três amigos, André, Bernardo e Carlos, moram em um condomínio fechado de uma cidade. O quadriculado representa a localização das ruas paralelas e perpendiculares, delimitando quadras de mesmo tamanho nesse condomínio, em que nos pontos A, B e C estão localizadas as casas de André, Bernardo e Carlos, respectivamente.

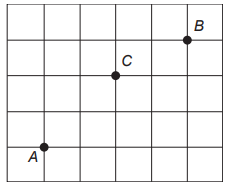
André deseja deslocar-se da sua casa até a casa de Bernardo, sem passar pela casa de Carlos, seguindo ao longo das ruas do condomínio, fazendo sempre deslocamentos para a direita ( → ) ou para cima ( ↑ ), segundo o esquema da figura. O número de diferentes caminhos que André poderá utilizar para realizar o deslocamento nas condições propostas é
A) 4.
B) 14.
C) 17.
D) 35.
E) 48.

Confira abaixo a resolução completa:

Solução comentada:

Este exercício quer saber quantas formas diferentes André tem para chegar na casa de Bernardo, sem passar pela casa de Carlos.

Logo, para fazermos uma análise como esta a forma mais fácil é você contabilizar todas as formas possíveis (incluindo aquelas que passam por Carlos) e depois descontar as possibilidades que passam pela casa de Carlos.

Portanto, no primeiro momento vamos calcular as possibilidades totais. Este é um exercício claro de permutação com repetição. Para os casos totais vamos ter 4 deslocamentos para a direita e 3 deslocamentos pra cima, sendo assim em nossa permutação:

P^{4,3}_7 = \frac{7!}{4!3!} = \frac{7*6*5*4!}{4!*3*2*1} = \frac{7* \not{6}*5*\not{4!}}{\not{4!}*\not{3}*\not{2}*\not{1}} = 7*5 = 35

Portanto, temos 35 possibilidades no total. Agora, vamos ter que calcular quantas são as possibilidades que passam pelo Carlos. Para isso, primeiro calculamos os caminhos de A até C, depois calculamos os caminhos de C até B, pois com essas duas contas vamos saber os caminhos totais que passam por C, uma vez que os caminhos até C não representam as possibilidades até B, que é o solicitado pelo exercício.

Para A até C, temos 2 deslocamentos a direita e 2 para cima, logo:

P^{2,2}_4 = \frac{4!}{2!2!} = \frac{4*3*2*1}{2*1*2*1} = \frac{\not{4}*3*2*1}{\not{2}*\not{1}*\not{2}*\not{1}}=3*2*1 = 6

Agora, para C até B, temos 2 deslocamentos pra a direita e 1 para cima, logo:

P^{2,1}_3 = \frac{3!}{2!} = \frac{3*2*1}{2*1} = \frac{3*\not{2}*1}{\not{2}*\not{1}}=3 

Agora, para sabermos as possibilidades totais multiplicamos um pelo outro:

P_{A\rightarrow C\rightarrow B } = 6*3 = 18

Por fim, descontamos os casos que passam por C dos casos totais, logo:

35 - 18 = 17

Sendo assim, a alternativa correta é c) 17.

Gabarito 142 ENEM 2020: C

Dica de conteúdo: Esse exercício utiliza de conceitos pontuais de permutação com repetição. Por isso, para conseguir solucionar exercícios como esse com mais facilidade, aconselhamos que você estude analise combinatória, mais precisamente para esse exercício o tópico de permutação. Este é um tópico que quase sempre cai no Enem. Por isso, fique atento.

Confira a resolução de todos os exercícios do Enem.

Confira aqui mais resoluções no site.

Quer tirar mais de 700 em Matemática no Enem?

Conheça o e-book onde você vai aprender todas as estratégias e macetes para conseguir resolver os exercícios de matemática do Enem de uma forma:

• Muito mais organizada;
• Mais rápida;
• Economizando contas;
• Analisando os exercícios.

Adquira já o seu aqui.