9 UNICENTRO 2021 ) Por diversos motivos de armazenagem, conforme pesquisa, as perdas médias de grãos, no país, chegam a aproximadamente 10% do total produzido anualmente.
Suponha que, em um silo, estão armazenados grãos de um determinado cereal, que começam a estragar com o passar do tempo, e a quantidade de grão bons para o consumo começa a decair. A tabela a seguir fornece dois instantes de tempo e as respectivas quantidades de grãos ainda em condições de consumo.
Sabendo que este decaimento ocorre segundo o modelo de uma função exponencial f : R → R tal que f(x) = bax, assinale a alternativa que apresenta, corretamente, a expressão f(x) que forneça, para este silo, a quantidade aproveitável de grãos (em toneladas) e que dependa do tempo após a estocagem x (em anos).
Confira abaixo a resolução completa:
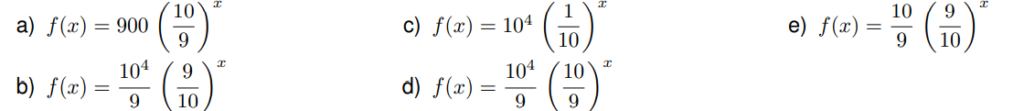
Solução comentada:
Temos claramente um exercício envolvendo equação e função exponencial, além de sistemas de equações.
O comando deste exercício é: assinale a alternativa que apresenta, corretamente, a expressão f(x) que forneça, para este silo, a quantidade aproveitável de grãos (em toneladas) e que dependa do tempo após a estocagem x (em anos).
Logo, temos que o modelo da expressão segundo o enunciado é:
f(x)=bax
Para encontrar os valores de a e b podemos utilizar a tabela dada e substituir os valores na função, desta forma vamos ter duas equações e duas incógnitas, assim conseguindo encontrar os valores por sistemas de equação.
Sendo assim, a tabela dada é:
Vamos então substituir os valores:
Primeiro o ponto 1:
f(x)=baxf(1)=1000=ba1f(1)=1000=ba
Agora o ponto 4:
f(x)=baxf(4)=729=ba4
Podemos então na primeira equação isolar o b em função do a, para conseguir encontrar o valor de a:
1000=baa1000=b
Sendo assim:
729=a1000∗a4729=1000∗a31000729=a109=a
Logo, tendo o valor de a conseguimos encontrar o valor de b:
a1000=b1091000=b910000=b9104=b
Sendo assim substituindo os valores na função teremos:
f(x)=baxf(x)=9104(109)x
Sendo assim, a alternativa que nos trás essa expressão é justamente a alternativa B.
