7 UNICENTRO 2021 – Sabendo que i =√(−1) é a unidade imaginária

7 UNICENTRO 2021 :

7 UNICENTRO 2021 ) Sabendo que i =√(−1) é a unidade imaginária, assinale a alternativa que apresenta, corretamente, o determinante da matriz

a) −i

b) −1

c) 0

d) i

e) 1

Confira abaixo a resolução completa:

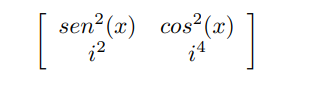
Solução comentada:

Temos claramente um exercício envolvendo matrizes, números complexos, álgebra e funções trigonométricas.

O comando do exercício quer saber o determinante da matriz.

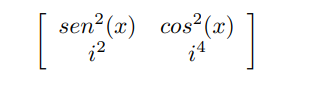
O determinante será o produto entre a diagonal principal menos o produto da diagonal inversa uma vez que é uma matriz 2×2:

sen^2(x)*i^4 -i^2*cos^2(x)\\

Temos que partindo dos números complexos:

• i²=-1;
• Logo i⁴ = (-1)²=1.

Sendo assim, substituindo:

sen^2(x)*1 -(-1)*cos^2(x)\\
\ \\
sen^2(x)+cos^2(x)\\

Sabemos que por propriedades de funções trigonométricas:

sen^2(x)+cos^2(x)=1\\

Logo, a alternativa que nos trás esta resposta é a alternativa E.

GABARITO 7 UNICENTRO 2021 : E.

Confira a resolução de todos os exercícios do Unicentro.

Confira aqui mais resoluções no site.

Quer tirar mais de 700 em Matemática no Enem?

Conheça o e-book onde você vai aprender todas as estratégias e macetes para conseguir resolver os exercícios de matemática do Enem de uma forma:

• Muito mais organizada;
• Mais rápida;
• Economizando contas;
• Analisando os exercícios.

Adquira já o seu aqui.