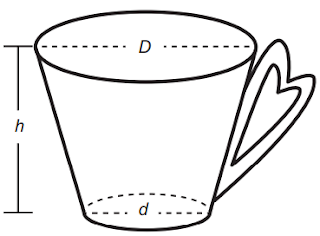
Sabe-se que 1 cm³ = 1 mL e que o topo da caneca é uma circunferência de diâmetro (D) medindo 10 cm, e a base é um círculo de diâmetro (d) medindo 8 cm. Além disso, sabe-se que a altura (h) dessa caneca mede 12 cm (distância entre o centro das circunferências do topo e da base).
Utilize 3 como aproximação para π.
Qual é a capacidade volumétrica, em mililitro, dessa caneca?
a) 216
b) 408
c) 732
d) 2 196
e) 2 928
Confira abaixo a resolução completa:
Solução comentada:
Temos claramente um exercício envolvendo geometria espacial.
O comando deste exercício é: Qual é a capacidade volumétrica, em mililitro, dessa caneca.
Logo, queremos saber qual a capacidade da caneca. Sabendo que as dimensões estão em cm e 1 cm³ = 1 mL.
Sendo assim, sabemos que o volume de um tronco de um cone é dado por:
V=\frac{\pi*h}{3}(R^2+R*r+r^2)Onde:
- h – altura do tronco;
- R – Raio maior;
- r – raio menor;
Como pi pode ser 3, temos que, substituindo os valores:
V=\frac{\pi*h}{3}(R^2+R*r+r^2)\\
\ \\
V=\frac{3*12}{3}(5^2+5*4+4^2)\\
\ \\
V=12(25+20+16)\\
\ \\
V=12*61=732Como o volume é 732, a alternativa correta é a letra C.
GABARITO 170 ENEM 2021: C.
Confira a resolução de todos os exercícios do Enem.
Confira aqui mais resoluções no site.
Quer tirar mais de 700 em Matemática no Enem?
Conheça o e-book onde você vai aprender todas as estratégias e macetes para conseguir resolver os exercícios de matemática do Enem de uma forma:
- Muito mais organizada;
- Mais rápida;
- Economizando contas;
- Analisando os exercícios.
Adquira já o seu aqui.





