169 ENEM 2020 DIGITAL) Uma casa lotérica oferece cinco opções de jogos. Em cada opção, o apostador escolhe um grupo de K números distintos em um cartão que contém um total de N números disponíveis, gerando, dessa forma, um total de C combinações possíveis para se fazer a marcação do cartão. Ganha o prêmio o cartão que apresentar os K números sorteados. Os valores desses jogos variam de R$ 1,00 a R$ 2,00, conforme descrito no quadro.
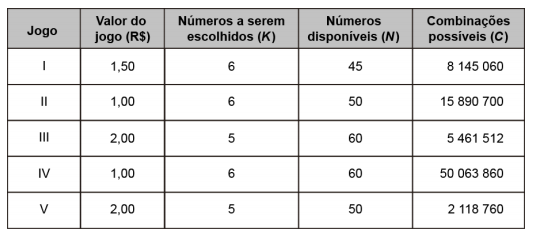
Um apostador dispõe de R$ 2,00 para gastar em uma das cinco opções de jogos disponíveis.
Segundo o valor disponível para ser gasto, o jogo que oferece ao apostador maior probabilidade de ganhar prêmio é o
a) I
b) II
c) III
d) IV
e) V
Confira abaixo a resolução completa:
Solução comentada:
O exercício quer saber “ o jogo que oferece ao apostador maior probabilidade de ganhar prêmio é o “.
Para isso sabemos que:
- O apostador tem R$ 2,00;
- Os dados do valor do jogo, números e combinações disponíveis estão na tabela.
Se liga na dica: esse exercício de cara assusta muitas pessoas, mas é simples. O exercício quer saber a maior probabilidade. O que é probabilidade? É uma divisão entre os casos de interesse divididos pelos casos totais. Por isso, aquele que tiver o maior resultado dessa divisão será o escolhido.
Como temos os casos totais dividindo, quanto menor for o número de combinações possíveis melhor, por isso já observamos que a III e a V são nossas favoritas.
A III terá apenas uma aposta, pois o valor de cada aposta é R$ 2,00, logo a probabilidade será:
P_{III}=\frac{1}{5.461.512}Já a V terá uma aposta também, pois o valor também é de R$ 2,00, logo a probabilidade será:
P_{V}=\frac{1}{2.118.760}Sendo assim, podemos encontrar que o resultado será aquele que tiver o maior número.
Partindo desse princípio, o escolhido é o V, da alternativa E.
Gabarito 169 ENEM 2020 DIGITAL: E
Confira a resolução de todos os exercícios do Enem.
Confira aqui mais resoluções no site.
Quer tirar mais de 700 em Matemática no Enem?
Conheça o e-book onde você vai aprender todas as estratégias e macetes para conseguir resolver os exercícios de matemática do Enem de uma forma:
- Muito mais organizada;
- Mais rápida;
- Economizando contas;
- Analisando os exercícios.
Adquira já o seu aqui.




