165 ENEM 2021 REAPLICAÇÃO)
165 ENEM 2021 REAPLICAÇÃO) Um casal decidiu aplicar em um fundo de investimentos que tem uma taxa de rendimento de 0,8% ao mês, num regime de capitalização composta.
O valor final F a ser resgatado, depois de n meses, a uma taxa de rendimento mensal x, é dado pela expressão algébrica F = C (1 + x)n, em que C representa o capital inicial aplicado.
O casal planeja manter a aplicação pelo tempo necessário para que o capital inicial de R$ 100 000,00 duplique, sem outros depósitos ou retiradas.
Fazendo uso da tabela, o casal pode determinar esse número de meses.
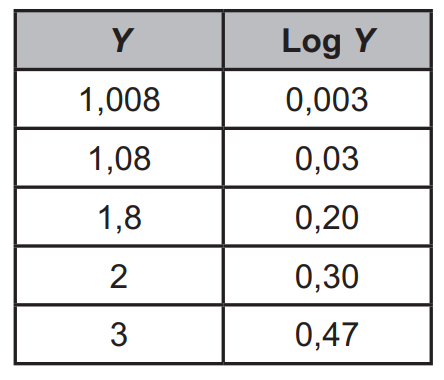
Para atender ao seu planejamento, o número de meses determinado pelo casal é
a) 156.
b) 125.
c) 100.
d) 10.
e) 1,5.
Solução comentada:
Temos claramente um exercício envolvendo pegadinha
O comando deste exercício é: Para atender ao seu planejamento, o número de meses determinado pelo casal é.
Queremos saber o número de meses para o casal atingir seu objetivo. Segundo o enunciado temos que:
- Taxa de 0,8% ao mês
- Vão aplicar R$ 100.000,00
- Querem dobrar o valor
- Expressão de juros é dada no enunciado
A expressão dos juros é:
M=C*(1+i)^t
Logo, sabemos que M que é o montante será o dobro de 100.000, que é C. Queremos descobrir o valor de t, e i é a taxa em valore decimais. Sendo assim, só precisamos solucionar esta equação exponencial:
200.000=100.000(1+0,008)^t\\ \ \\ 2=1,008^t\\ \ \\ para\ resolver\ aplicamos\ log\ dos\ dois\ lados:\\ \ \\ log(2)=log(1,008^t)\\
Aplicando propriedade de logaritmo o t passa multiplicando o log:
log(2)=log(1,008^t)\\
\ \\
log(2)=t*log(1,008)\\
\ \\
utilizando\ os\ valores\ da\ tabela:\\
\ \\
0,3=t*0,003\\
\ \\
\frac{0,3}{0,003}=t\\
\ \\
100=tComo t vale 100, a alternativa correta é a letra C.
GABARITO 165 ENEM 2021 REAPLICAÇÃO: C.
Confira a resolução de todos os exercícios do Enem.
Confira aqui mais resoluções no site.
Quer tirar mais de 700 em Matemática no Enem?
Conheça o e-book onde você vai aprender todas as estratégias e macetes para conseguir resolver os exercícios de matemática do Enem de uma forma:
- Muito mais organizada;
- Mais rápida;
- Economizando contas;
- Analisando os exercícios.
Adquira já o seu aqui.





