170 Enem 2020 PPL – Dois atletas partem de pontos

170 ENEM 2020 PPL)  Dois atletas partem de pontos, respectivamente P₁ e P₂ , em duas pistas planas distintas, conforme a figura, deslocando-se no sentido anti-horário até a linha de chegada, percorrendo, desta forma, a mesma distância (L). Os trechos retos dos finais das curvas até a linha de chegada desse percurso têm o mesmo comprimento (l) nas duas pistas e são tangentes aos trechos curvos, que são semicírculos de centro C. O raio do semicírculo maior é R₁ e o raio do semicírculo menor é R₂ .

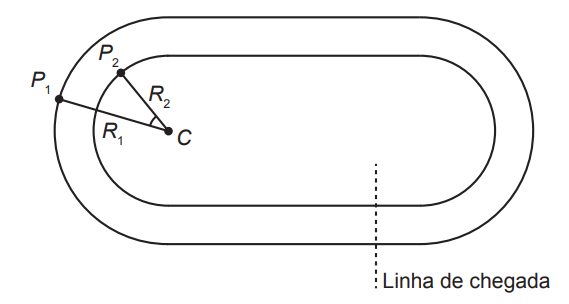
Sabe-se que o comprimento de um arco circular é dado pelo produto do seu raio pelo ângulo, medido em radiano, subentendido pelo arco. Nas condições apresentadas, a razão da medida do ângulo P₂CP₁ pela diferença L− I é dada por

a) R₂ – R₁ 

b) 1/R₁ – 1/R₂

c) 1/R₂ – 1/R₁

d) 1 / (R₂ – R₁)

e) 1/R₁ + 1/R₂

Confira abaixo a resolução completa:

Solução comentada:

O exercício quer saber ” a razão da medida do ângulo P₂CP₁ pela diferença L− I é dada por“.

Se liga na dica: temos claramente um exercício que envolve geometria e circunferências. Nesse exercício vamos precisar enxergar basicamente nossas grandezas para assim podermos fazer o cálculo da razão dos valores.

Segundo o enunciado:

• Os atletas parte do ponto P1 e P2 respectivamente;
• Deslocam-se no sentido anti-horário;
• Percorrem a mesma distância L;
• Os trechos retos tem a mesma distância l;
• O raio do círculo maior é R1 e do menor é R2;
• O comprimento de um arco circular é dado pelo produto do raio pelo seu ângulo medido em radiano;

Feito isso, podemos colocar essas informações todas no desenho. No caso também denominamos como d1 o arco do atleta 1 e o d2 o arco do atleta 2, além disso definimos os ângulos g e o para o respectivo desenho como podemos ver abaixo.

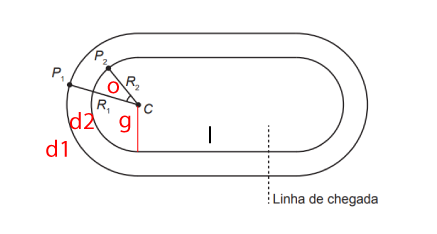
Nota-se que o ângulo P2CP1 é justamente o ângulo o.

Sabemos que a distância total percorrida pelo atleta 1 será:

L=d_1+l

Sabemos que a distância total percorrida pelo atleta 2 será:

L=d_2+l

Como as distâncias L são iguais e l também, podemos afirmar que:

d_1=d_2

Sabemos que as distâncias dos arcos são dadas pelos produtos do ângulo pelo raio, podemos definir então que:

• d1 será o produto do ângulo g com o raio 1;
• d2 será o produto da soma dos ângulos o e g com o raio 2.

Sendo assim:

g*R_1=(g+o)*R_2

Podemos com essa última equação então definir quem é o ângul o, para assim calcular a razão. Portanto vamos isolá-lo:

g*R_1=(g+o)*R_2\\
\ \\
g*R_1=g*R_2+o*R_2\\
\ \\
g*R_1-g*R_2=o*R_2\\
\ \\
\frac{g*R_1-g*R_2}{R_2}=o

Sabendo então quem é o basta saber quem é L-l. Como sabemos que L é igual a soma das distâncias de arco com a distância l, podemos afirmar que:

L=l+d_1\\
\ \\
L-l=d_1

Portanto, sabemos que L-l é igual a d1, sendo assim podemos calcular a razão:

\frac{P2CP1}{L-l}=\frac{o}{L-l}=\frac{\frac{g*R_1-g*R_2}{R_2}}{d_1}

Mas sabemos que d1 é o produto entre o ângulo g e R1, logo:

\frac{\frac{g*R_1-g*R_2}{R_2}}{d_1}=\frac{\frac{g*R_1-g*R_2}{R_2}}{g*R_1}\\
\ \\
\frac{g*R_1-g*R_2}{R_2*g*R_1}\\
\ \\

Simplificando agora temos que:

\frac{g*R_1-g*R_2}{R_2*g*R_1}=\frac{\not{g}*\not{R_1}}{R_2*\not{g}*\not{R_1}}-\frac{\not{g}*\not{R_2}}{\not{R_2}*\not{g}*R_1}\\
\ \\
\frac{1}{R_2}-\frac{1}{R_1}

Logo a alternativa que me trás esta expressão é justamente a alternativa c.

Gabarito 170 ENEM 2020 PPL: C

Confira a resolução de todos os exercícios do Enem.

Confira aqui mais resoluções no site.

Quer tirar mais de 700 em Matemática no Enem?

Conheça o e-book onde você vai aprender todas as estratégias e macetes para conseguir resolver os exercícios de matemática do Enem de uma forma:

• Muito mais organizada;
• Mais rápida;
• Economizando contas;
• Analisando os exercícios.

Adquira já o seu aqui.