165 ENEM 2020 PPL) A taxa de mortalidade infantil vem decaindo a cada ano no Brasil. O gráfico, gerado a partir de dados do IBGE, apresenta a evolução da taxa de mortalidade infantil (número de óbitos para cada 1 000 nascidos vivos) de crianças com até 5 anos, no Brasil, no período de 2000 a 2011.
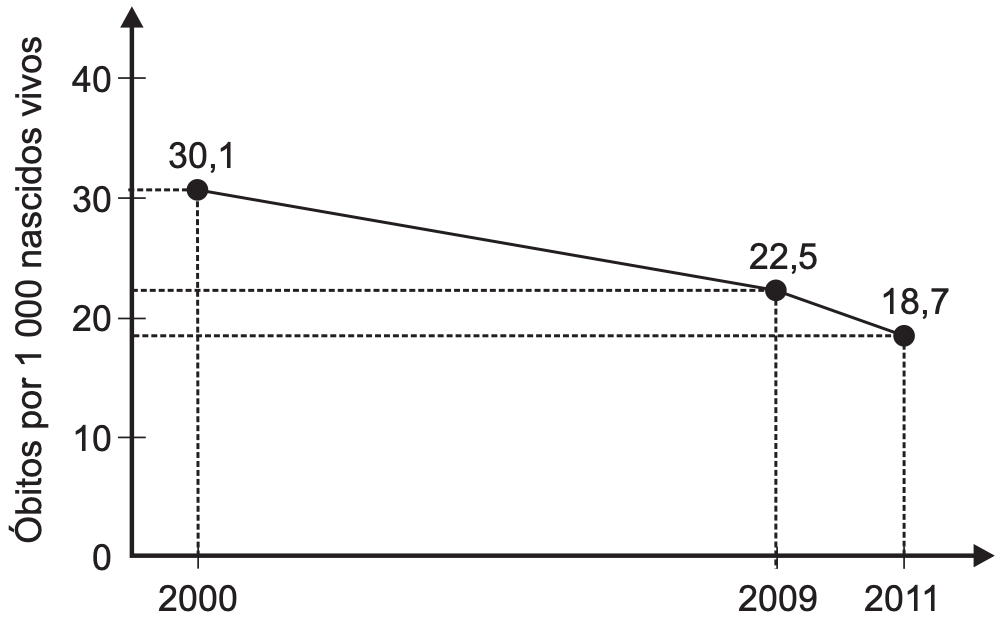
Considere que, para os próximos anos, o decréscimo anual médio do número de óbitos para cada 1 000 nascidos vivos registrado, no período de 2009 a 2011, será mantido.
A partir das informações fornecidas, a taxa de mortalidade infantil de crianças com até 5 anos tornar-se-á inferior a 10 no período de
a) 2011 a 2012.
b) 2012 a 2013.
c) 2013 a 2014.
d) 2015 a 2016.
e) 2017 a 2018.
Confira abaixo a resolução completa:
Solução comentada:
O exercício quer saber “ a taxa de mortalidade infantil de crianças com até 5 anos tornará-se inferior a 10″.
Se liga na dica: temos claramente um exercício de análise de gráfico e porcentagem. Neste exercício vamos ter de calcular qual é a nova taxa de mortalidade infantil de crianças com até 5 anos para saber quando ser tornará inferior a 10, sabendo que o decréscimo de 2009 até 2011 será mantido.
Primeiramente vamos ter de calcular a redução anual no período de 2009 a 2011. Para isso calculamos a diferença e dividimos por 2 (duas reduções).
Calculando a diferença:
22,5-18,7=3,8
Sabendo que o decréscimo foi de 3,8, agora vamos descobrir quanto reduziu por ano:
\frac{3,8}{2}=1,9Como queremos que seja menor que 10, vamos precisar descobrir quantas reduções será necessário para chegar a menos que 10:
18,7-1,9=16,8\\ \ \\ 16,8-1,9=14,9\\ \ \\ 14,9-1,9=13\\ \ \\ 13-1,9=11,1\\ \ \\ 11,1-1,9=9,2
Como serão necessários 5 reduções, a partir de 2011 precisamos contar 5 anos, então no caso vai ser no ano de 2016.
Se é no ano de 2016, a alternativa correta é a letra D.
Gabarito 165 ENEM 2020 PPL: D
Confira a resolução de todos os exercícios do Enem.
Confira aqui mais resoluções no site.
Quer tirar mais de 700 em Matemática no Enem?
Conheça o e-book onde você vai aprender todas as estratégias e macetes para conseguir resolver os exercícios de matemática do Enem de uma forma:
- Muito mais organizada;
- Mais rápida;
- Economizando contas;
- Analisando os exercícios.
Adquira já o seu aqui.




