8 UNICENTRO 2020 – Na figura, ABCD é um quadrado com 2cm de lado

8 UNICENTRO 2020 :

8 UNICENTRO 2020) Na figura, ABCD é um quadrado com 2cm de lado, E e G são os pontos médios dos lados DC e AD, respectivamente, e a circunferência é tangente aos lados AB e BC do quadrado grande. Se a área do círculo mede xpicm² , então o valor de x é

A) 4 –√2

B) 4 + √2

C) 4 + 6√2

D) 6 – 4√2

E) 6 + 4√2

Confira abaixo a resolução completa:

Solução comentada:

Temos claramente um exercício envolvendo geometria espacial e álgebra.

O comando deste exercício é: Se a área do círculo mede xpicm² , então o valor de x é.

Logo o exercício quer saber o valor de x, sabendo que a área da circunferência é xpicm².

Temos então que, a área de uma circunferência é dada por:

A=\pi r^2\\
\ \\
Logo:\\
\ \\

x*pi=\pi r^2\\
\ \\
x=r^2

Sendo assim para encontrar quem é x basta encontrar quem é r^2.

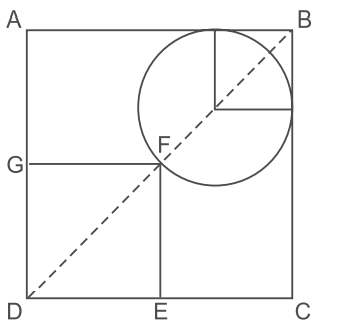
Outra informação que temos é que os lados do quadrado medem 2 m, portanto podemos aproveitar essa informação e traçarmos um plano cartesiano:

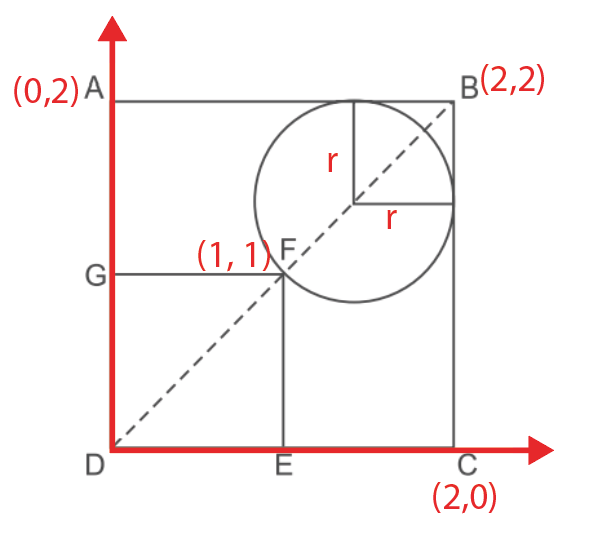
Além disso também colocamos no plano cartesiano o raio da circunferência.

Os nossos pontos da circunferência são B(2, 2), C(2, 0) e A(0, 2).

Outro ponto que podemos destacar é F, que será (1, 1).

O QUE VAMOS FAZER:

Vamos definir uma equação para a circunferência em função de r, vamos substituir o ponto F, uma vez que a circunferência passa por ele, e depois vamos encontrar quem é o raio.

Para equacionarmos a circunferência vamos definir seu centro. O centro será dado por:

x0 = 2 – r.

y0 = 2 – r.

Sendo assim a equação geral da circunferência fica:

(x-x_0)^2+(y-y_0)^2=r^2\\
\ \\
(x-(2-r))^2+(y-(2-r))^2=r^2\\
\ \\

Como mencionamos anteriormente, a circunferência passa pelo ponto F, portanto vamos substituir ele na equação para encontrar r:

(1-(2-r))^2+(1-(2-r))^2=r^2\\
\ \\
2(r-1)^2=r^2\\
\ \\
2(r^2-2r+1)=r^2\\
\ \\
2r^2-4r+2=r^2\\
\ \\
r^2-4r+2=0\\

Podemos encontrar o r por Bhaskara:

r=\frac{-(-4)\pm\sqrt{(-4)^2-4*1*2}}{2*1}\\
 \ \\
r=\frac{4\pm\sqrt{8}}{2}\\
 \ \\
r=\frac{4\pm2\sqrt{2}}{2}\\
 \ \\
r'=2+\sqrt{2}\\
 \ \\
r''=2-\sqrt{2}\\

O raio não pode ser maior que 2, uma vez que o lado do quadrado vale 2. Logo o raio é o segundo valor.

Portanto para encontrar o valor de x:

x=r^2\\
\ \\
x=(2-\sqrt{2})^2
\ \\
x=4-4\sqrt{2}+2
\ \\
x=6-4\sqrt{2}

Logo a alternativa correta é a letra D.

GABARITO 8 UNICENTRO 2020 : D.

Confira a resolução de todos os exercícios do Unicentro.

Confira aqui mais resoluções no site.

Quer tirar mais de 700 em Matemática no Enem?

Conheça o e-book onde você vai aprender todas as estratégias e macetes para conseguir resolver os exercícios de matemática do Enem de uma forma:

• Muito mais organizada;
• Mais rápida;
• Economizando contas;
• Analisando os exercícios.

Adquira já o seu aqui.