33 UEPG 2019 VERÃO – Sendo a e b raízes naturais do polinômio P(x)

33 UEPG 2019 VERÃO:

33 UEPG 2019 VERÃO) Sendo a e b raízes naturais do polinômio P(x) = x^4 + 2x^3 – 9x² – 2x + 8, onde a < b. Considerando que o triângulo retângulo BAC, reto em A, tem AB = a + 2, AC = b + 2 e AĈB = α , assinale o que for correto.

01) secα =4/5.

02) senα + cosα = 7/5.

04) A hipotenusa BC = 5.

08) tgα =4/3.

Confira abaixo a resolução completa:

Solução comentada:

Temos claramente um exercício envolvendo funções, triângulos e funções trigonométricas

Observando as alternativas, vamos precisar do valor de α. Sabemos que α é igual ao ângulo C do triângulo ACB. Onde precisamos dos valores de a e b para identificar os lados do triângulo.

Sendo assim a primeira coisa que devemos fazer é identificar quem é a e b.

O nosso polinômio de grau 4 é:

P(x)=x^4+2x^3-9x^2-2x+8

Sabemos que: a e b raízes naturais do polinômio, onde a < b.

Logo, vamos ter duas raízes naturais neste polinômio. A menor será a e a maior será b.

Como identificar a raiz desse polinômio?

DICA: sempre que temos um polinômio de grau 4 ou 3 em uma prova de vestibular, uma das raízes na maioria das vezes será -1 ou 1.

Sendo assim vamos testar x=1:

P(1)=1^4+2*1^3-9*1^2-2*1+8=0

Logo x=1 é raíz do polinômio. Como é um número natural já sabemos que será uma das raízes naturais que estamos buscando.

Vamos testar agora x=-1:

P(-1)=(-1)^4+2*(-1)^3-9*(-1)^2-2*(-1)+8=0

Sendo assim x=-1 também é raíz do polinômio. Porém como não é natural, não será um valor de a e b.

Logo, precisamos encontrar outra nariz natural ainda.

Podemos dividir o polinômio P(x) pelos binômios de x=1 e x=-1, assim vamos encontrar um polinômio de grau 2 que vai nos dar as duas raízes restantes.

Sendo assim vamos ter a seguinte divisão:

\frac{x^4+2x^3-9x^2-2x+8}{(x-1)(x+1)}

Essa divisão pode ser feita por briot-ruffini ou método de chaves. Para a resolução não ficar muito longa, uma vez que falta muita coisa, vamos lhe dar o resultado final da divisão:

\frac{x^4+2x^3-9x^2-2x+8}{(x-1)(x+1)}=x^2+2x-8

Logo, com esse polinômio agora podemos aplicar bháskara para encontrar as duas raízes que faltam para encontramos a e b.

Sendo assim, encontrando as raízes através de bháskara:

x=\frac{-2\pm \sqrt{2^2-4*1*(-8)}}{2*1}=\frac{-2\pm \sqrt{36}}{2}\frac{-2\pm6}{2}\\
\ \\
x'=2\\
 \ \\
x''=-4

Sendo assim, como queremos as raízes naturais, a raiz que nos interessa é x=2.

Logo, nossas duas raízes naturais são:

• x=1;
• x=2.

Como sabemos que a<b, podemos afirmar que:

• a=1;
• b=2.

Logo, podemos identificar os lados do triângulo para dar sequência a resolução:

Como fazer?

Temos as seguintes informações: AB = a + 2, AC = b + 2 e AĈB = α. E também que é um triângulo retângulo em A.

Encontrando os lados:

AB=a+2=1+2=3\\
\ \\
AC=b+2=2+2=4

Desenhando nosso triângulo ABC:

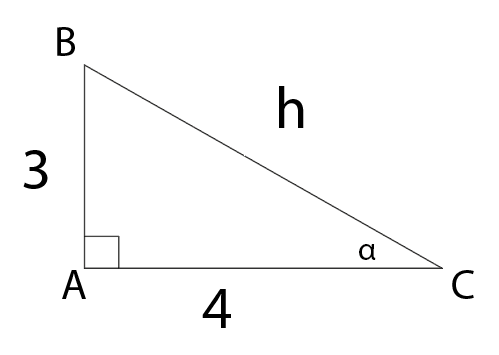
Como uma das alternativas quer saber o valor da hipotenusa, já vamos calculá-la. Assim também conseguimos encontrar o valor do ângulo α.

h^2=3^2+4^2\\
\ \\
h=\sqrt{9+16}\\
\ \\
h=\sqrt{25}\\
\ \\
h=BC=5

Sabendo o valor da hipotenusa, podemos perceber que não vamos conseguir calcular o valor de α sem o auxílio de uma calculadora. Mas também nem será necessário. Vamos as alternativas.

01) secα =4/5.

Sabemos que secante é a inversa do cosseno, logo:

sec(α)=\frac{1}{cos(α)}\\

Sabemos que cos α é:

cos(α)=\frac{4}{5}

Logo:

sec(α)=\frac{1}{cos(α)}=\frac{1}{\frac{4}{5}}=\frac{5}{4}

Sendo assim a 01 está incorreta.

02) senα + cosα = 7/5.

Sabemos já o cos α, agora encontrando o sen α:

sen(α)=\frac{3}{5}

Logo, realizando a soma:

sen(α)+cos(α)=\frac{3}{5}+\frac{4}{5}=\frac{7}{5}

Sendo assim a 02 está correta.

04) A hipotenusa BC = 5.

Como calculamos anteriormente, a hipotenusa h=BC=5.

Sendo assim a 04 está correta.

08) tgα =4/3.

Encontrando a tangente:

tg(α)=\frac{3}{4}

Sendo assim a 08 está correta.

Logo o gabarito será: 02+04=06.

GABARITO 33 UEPG 2019 VERÃO: 6.

Confira a resolução de todos os exercícios do Enem.

Confira aqui mais resoluções no site.

aqui mais resoluções no site.

Quer tirar mais de 700 em Matemática no Enem?

Conheça o e-book onde você vai aprender todas as estratégias e macetes para conseguir resolver os exercícios de matemática do Enem de uma forma:

• Muito mais organizada;
• Mais rápida;
• Economizando contas;
• Analisando os exercícios.

Adquira já o seu aqui.