31 UEPG 2018 INVERNO – Sabendo que um losango e um quadrado

31 UEPG 2018 INVERNO:

31 UEPG 2018 INVERNO) Sabendo que um losango e um quadrado têm o mesmo perímetro, e que d e D representam, respectivamente, as medidas das diagonais menor e maior do losango. Considerando ainda que d/D=4/9 e que D – d = 30, assinale o que for correto.

01) A área do quadrado é maior que a área do losango.

02) A diagonal maior do losango mede 54.

04) A área do losango mede 1296.

08) A razão entre a área do quadrado e a área do losango é de 97/72.

Confira abaixo a resolução completa:

Solução comentada:

Temos claramente um exercício envolvendo geometria plana, áreas e razão.

Antes de resolvermos as sentenças, vamos primeiramente desenhar as duas figuras.

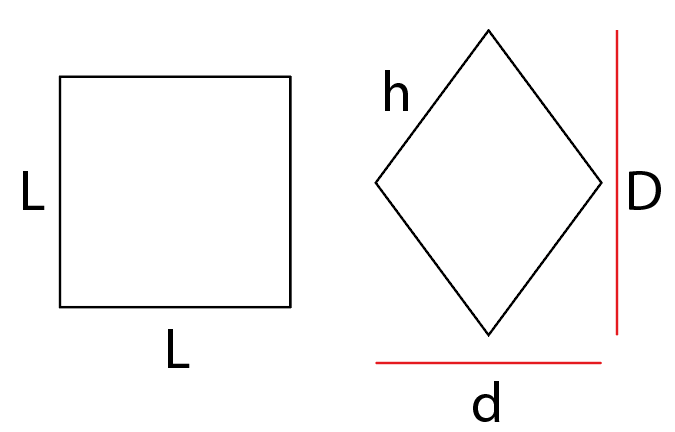
Como as sentenças tratam das áreas das figuras e também dos valores das diagonais, vamos primeiramente encontrar esses valores para então resolver as alternativas.

Para encontrar as diagonais temos duas equações dadas no enunciado:

• d/D=4/9 e que D – d = 30

Com a primeira podemos isolar d:

\frac{d}{D}=\frac{4}{9}\\
\ \\
d=\frac{4D}{9}\\

Sendo assim, podemos substituir na segunda equação para encontrar o valor de D:

D-d=30\\
\ \\
D-\frac{4D}{9}=30\\
\ \\
\frac{5D}{9}=30\\
\ \\
D=\frac{30*9}{5}\\
\ \\
D=54

Podemos definir d:

d=\frac{4D}{9}=\frac{4*54}{9}\\
\ \\
d=24

Com os valores de d e D podemos calcular a área do losango:

A_L=\frac{d*D}{2}=\frac{24*54}{2}\\
 \ \\
A_L=648

Com os valores dos lados do losango, podemos definir o valor do lado do quadrado, pois segundo o enunciado temos que:

• losango e um quadrado tem o mesmo perímetro.

Logo, isso quer dizer que:

4L=4h\\
\ \\
L=h

Se o lado do quadrado é igual ao lado do losango, que vale h, podemos encontrar o valor de h através de pitágoras, que será o valor de h.

Vale destacar que a área do quadrado é dada por:

A_Q=L^2=h^2

Para achar o lado do losango temos que:

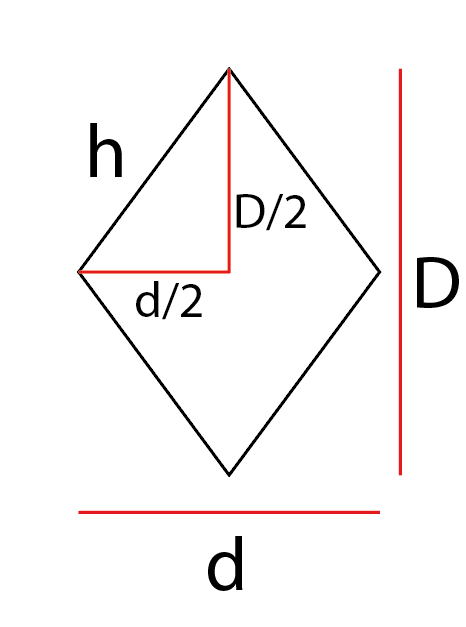
Sendo assim por pitágoras:

h^2=(\frac{D}{2})^2+(\frac{d}{2})^2

Se observamos h² é a área do quadrado, logo:

A_Q=(\frac{D}{2})^2+(\frac{d}{2})^2\\
\ \\
A_Q=(\frac{54}{2})^2+(\frac{24}{2})^2\\
\ \\
A_Q=27^2+12^2\\
\ \\
A_Q=729+144\\
\ \\
A_Q=873

Sendo assim temos os seguintes dados:

D=54\\
\ \\
d=24\\
\ \\
A_L=648\\
\ \\
A_Q=873

Vamos para as sentenças.

01) A área do quadrado é maior que a área do losango.

Temos que a área do quadrado vale 873 e a área do losango vale 648. Logo:

A_Q > A_L.

Sendo assim a 01 está correta.

02) A diagonal maior do losango mede 54.

Verdadeiro, D=54.

Sendo assim a 02 está correta.

04) A área do losango mede 1296.

Falso, A_L=648.

Sendo assim a 04 está incorreta.

08) A razão entre a área do quadrado e a área do losango é de 97/72.

Vamos calcular:

\frac{A_Q}{A_L}=\frac{873}{648}=\frac{97}{72}

Sendo assim a 08 está correta.

Logo o gabarito é: 01+02+08=11.

GABARITO 31 UEPG 2018 INVERNO: 11.

Confira a resolução de todos os exercícios do Enem.

Confira aqui mais resoluções no site.

aqui mais resoluções no site.

Quer tirar mais de 700 em Matemática no Enem?

Conheça o e-book onde você vai aprender todas as estratégias e macetes para conseguir resolver os exercícios de matemática do Enem de uma forma:

• Muito mais organizada;
• Mais rápida;
• Economizando contas;
• Analisando os exercícios.

Adquira já o seu aqui.