180 ENEM 2020) Pergolado é o nome que se dá a um tipo de cobertura projetada por arquitetos, comumente em praças e jardins, para criar um ambiente para pessoas ou plantas, no qual há uma quebra da quantidade de luz, dependendo da posição do sol. É feito como um estrado de vigas iguais, postas paralelas e perfeitamente em fila, como ilustra a figura.

Um arquiteto projeta um pergolado com vãos de 30 cm de distância entre suas vigas, de modo que, no solstício de verão, a trajetória do sol durante o dia seja realizada num plano perpendicular à direção das vigas, e que o sol da tarde, no momento em que seus raios fizerem 30° com a posição a pino, gere a metade da luz que passa no pergolado ao meio-dia.
Para atender à proposta do projeto elaborado pelo arquiteto, as vigas do pergolado devem ser construídas de maneira que a altura, em centímetro, seja a mais próxima possível de
a) 9.
b) 15.
c) 26.
d) 52.
e) 60.
Confira abaixo a resolução completa:
Solução comentada:
O exercício quer saber a altura das vigas do pergolado.
Para isso a altura deve atender que quando os raios fizerem 30° com a posição a pino, gere a metade da luz que passa no pergolado ao meio-dia.
Para gerar metade da luz, ele deverá iluminar metade do espaço entre as vigas.
Como o espaço é de 30 cm, ele deve iluminar apenas 15 cm.
Quando o sol estiver nessa condição teremos uma situação com a figura abaixo.
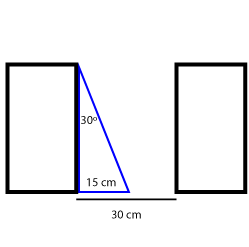
Para calcular a altura do pergolado nessa condição basta utilizarmos tangente:
tg(30)=\frac{15}{h}\\
\ \\
h=\frac{15}{tg(30)}\\
\ \\
como\ tg(30)=\frac{\sqrt3}{3}\\
\ \\
h = \frac{15}{\frac{\sqrt3}{3}}\\
\ \\
h = \frac{15*3}{\sqrt3}\\
\ \\
multiplicando\ por\ raiz\ de\ 3\ em\ cima\ e\ em \ baixo:\\
\ \\
h = \frac{15*3*\sqrt3}{\sqrt3\sqrt3}\\
\ \\
h = \frac{15*3*\sqrt3}{3}\\
\ \\
h =15*\sqrt3\\Como não temos nenhuma reposta com essa expressão, podemos analisar que raiz de 3 fica entre 1,5 e 2 (já que 1,5*1,5 = 2,25 e 2*2 = 4). Logo, utilizando um valor do meio que é 1,75:
15*1,75=26,25
Portanto a resposta é a alternativa c) 26
Gabarito 180 ENEM 2020: C
Confira a resolução de todos os exercícios do Enem.
Confira aqui mais resoluções no site.
Quer tirar mais de 700 em Matemática no Enem?
Conheça o e-book onde você vai aprender todas as estratégias e macetes para conseguir resolver os exercícios de matemática do Enem de uma forma:
- Muito mais organizada;
- Mais rápida;
- Economizando contas;
- Analisando os exercícios.
Adquira já o seu aqui.




