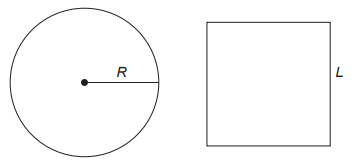
173 ENEM 2020 PPL) Um vidraceiro precisa construir tampos de vidro com formatos diferentes, porém com medidas de áreas iguais. Para isso, pede a um amigo que o ajude a determinar uma fórmula para o cálculo do raio R de um tampo de vidro circular com área equivalente à de um tampo de vidro quadrado de lado L.
A fórmula correta é
a) R = L / √π
b) R = L / √2π
c) R = L² / 2π
d) R = √(2L/π)
e) R = 2 √(L/π)
Confira abaixo a resolução completa:
Solução comentada:
O exercício quer saber “ A fórmula correta “.
Se liga na dica: temos claramente um exercício de geometria plana. Neste exercício vamos precisar relacionar o Raio da circunferência com o lado do quadrado para que tenhamos uma área equivalente, isto é, a mesma área.
Logo vamos precisar equacionar e igualar a área da circunferência com a área do quadrado.
Sendo assim:
\pi*R^2=L*L\\
\ \\
R^2=\frac{L^2}{\pi}\\
\ \\
R=\sqrt{\frac{L^2}{\pi}}\\
\ \\
R={\frac{L}{\sqrt{\pi}}}\\Logo a alternativa que nos trás a expressão correta é a letra A.
Gabarito 173 ENEM 2020 PPL: A
Confira a resolução de todos os exercícios do Enem.
Confira aqui mais resoluções no site.
Quer tirar mais de 700 em Matemática no Enem?
Conheça o e-book onde você vai aprender todas as estratégias e macetes para conseguir resolver os exercícios de matemática do Enem de uma forma:
- Muito mais organizada;
- Mais rápida;
- Economizando contas;
- Analisando os exercícios.
Adquira já o seu aqui.




