156 PROVA AMARELA ENEM 2020)
A Lei de Zipf, batizada com o nome do linguista americano George Zipf, é uma lei empírica que
relaciona a frequência ( f ) de uma palavra em um dado texto com o seu ranking (r). Ela é dada por
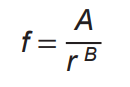
O ranking da palavra é a sua posição ao ordenar as palavras por ordem de frequência. Ou seja, r = 1 para a
palavra mais frequente, r = 2 para a segunda palavra mais frequente e assim sucessivamente. A e B são constantes positivas.
Diponível em: http://klein.sbm.org.br. Acesso em: 12 ago. 2020 (adatpado).
Com base nos valores de X = log (r) e Y = log ( f ) , é possível estimar valores para A e B. No caso hipotético em que a lei é verificada exatamente, a relação entre Y e X é
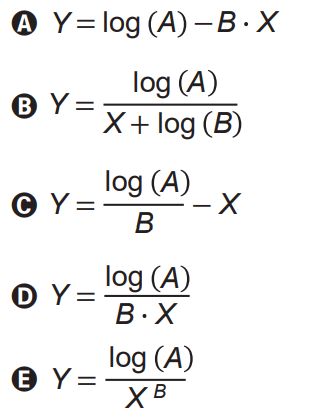
Confira abaixo a resolução completa:
Solução comentada:
O exercício quer saber uma “relação entre Y e X“.
Para isso, sabemos que x = log(r), e y = log(f).
Portanto, vamos ter de fazer as operações com a equação dada pelo exercício, temos:
f = \frac{A}{r^B}\\
\ \\
vamos\ aplicar\ logaritmo\ nos\ dois\ lados\ da\ equação: \\
\ \\
log(f) = log(\frac{A}{r^B})\\
\ \\
aplicando\ propriedade\ de\ logaritmo\ ,\ logaritmo\ da\ divisão\ é\ subtração\ dos\ logaritmos: \\
\ \\
log(f) = log(A)-log(r^B)\\
\ \\
aplicando\ outra\ propriedade\ ,\ temos: \\
\ \\
log(f) = log(A)-B*log(r)\\
\ \\
como\ sabemos\ que:\ x=log(r)\ e\ y=log(f)\ temos\ que:\\
\ \\
y = log(A)-B*X
Portanto, alternativa correta é a letra A) y = log(A) – B*x
Gabarito 156 ENEM 2020: A
Dica de conteúdo: Neste exercício utilizamos conceitos de logaritmo e equações exponenciais. Este é um tema que costumeiramente também cai bastante no Enem, não sendo cobrado vários exercícios, mas pelo menos um exercício sempre cai. Geralmente é apenas para saber aplicar as propriedades de logaritmo, devido a isso é muito importante que você entenda as propriedades de logaritmo.
Confira a resolução de todos os exercícios do Enem.
Confira aqui mais resoluções no site.
Quer tirar mais de 700 em Matemática no Enem?
Conheça o e-book onde você vai aprender todas as estratégias e macetes para conseguir resolver os exercícios de matemática do Enem de uma forma:
- Muito mais organizada;
- Mais rápida;
- Economizando contas;
- Analisando os exercícios.
Adquira já o seu aqui.




