149 ENEM 2020 DIGITAL) Uma empresa deseja construir um edifício residencial de 12 pavimentos, num lote retangular de lados medindo 22 e 26 m. Em 3 dos lados do lote serão construídos muros. A frente do prédio será sobre o lado do lote de menor comprimento. Sabe-se que em cada pavimento 32 m² serão destinados à área comum (hall de entrada, elevadores e escada), e o restante da área será destinado às unidades habitacionais. A legislação vigente exige que prédios sejam construídos mantendo distâncias mínimas dos limites dos lotes onde se encontram. Em obediência à legislação, o prédio ficará 5 m afastado da rua onde terá sua entrada, 3 m de distância do muro no fundo do lote e 4 m de distância dos muros nas laterais do lote, como mostra a figura.
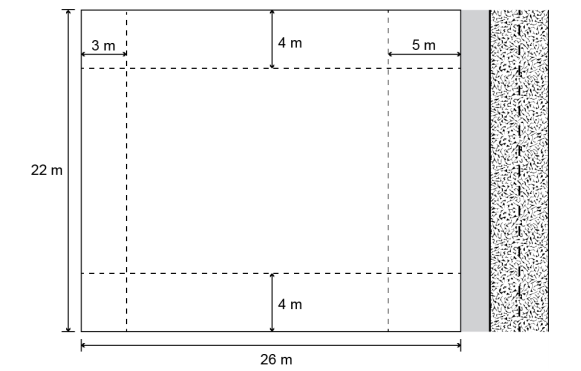
A área total, em metro quadrado, destinada às unidades habitacionais desse edifício será de
a) 2 640.
b) 3 024.
c) 3 840.
d) 6 480.
e) 6 864.
Confira abaixo a resolução completa:
Solução comentada:
O exercício quer saber “área total, destinadas as unidades habitacionais. ”
Para saber a área total vamos ter que calcular a área dos 12 pavimentos. Para encontrar a área dos 12 pavimentos primeiramente vamos ter que calcular a área de 1 pavimento.
Para calcular a área habitacional de cada pavimento sabemos que 32 m² são destinadas a área comum.
Logo, calculando a área de cada pavimento será o produto entre os lados descontando a distância para as laterais:
A=(26-3-5)*(22-4-4)=18*14=252m²
Tendo essa área, precisamos descontar a área comum:
A_P=252-32=220m²
Sabendo a área de um pavimento, basta multiplicar por 12 para termos a área total habitacional dos 12 pavimentos:
A_T=220*12=2640m²
Logo a alternativa correta é a letra a) 2640.
Gabarito 149 ENEM 2020 DIGITAL: A
Confira a resolução de todos os exercícios do Enem.
Confira aqui mais resoluções no site.
Quer tirar mais de 700 em Matemática no Enem?
Conheça o e-book onde você vai aprender todas as estratégias e macetes para conseguir resolver os exercícios de matemática do Enem de uma forma:
- Muito mais organizada;
- Mais rápida;
- Economizando contas;
- Analisando os exercícios.
Adquira já o seu aqui.




