138 PROVA AMARELA ENEM 2020)
Um clube deseja produzir miniaturas em escala do troféu que ganhou no último campeonato. O troféu está representado na Figura 1 e é composto por uma base em formato de um paralelepípedo reto-retângulo de madeira, sobre a qual estão fixadas três hastes verticais que sustentam uma esfera de 30 cm de diâmetro, que fica centralizada sobre a base de madeira. O troféu tem 100 cm de altura, incluída sua base.
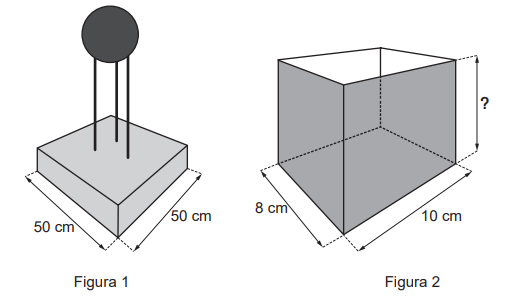
A miniatura desse troféu deverá ser instalada no interior de uma caixa de vidro, em formato de paralelepípedo reto-retângulo, cujas dimensões internas de sua base estão indicadas na Figura 2, de modo que a base do troféu seja colada na base da caixa e distante das paredes laterais da caixa de vidro em pelo menos 1 cm. Deve ainda haver uma distância de exatos 2 cm entre o topo da esfera e a tampa dessa caixa de vidro. Nessas condições deseja-se fazer a maior miniatura possível. A medida da altura, em centímetro, dessa caixa de vidro deverá ser igual a
A) 12.
B) 14.
C) 16.
D) 18.
E) 20
Confira abaixo a resolução completa:
Solução comentada:
Neste exercício é solicitado para que seja calculado a medida em altura da caixa vidro, dando as condições para que o troféu possa ser colocado dentro da caixa.
A primeira informação que temos é que as medidas da base da caixa são de 8CM e 10CM.
O exercício ainda destaca que a base do troféu deve deixar uma distância de pelo menos 1 cm entre o troféu e as extremidades da caixa.
Logo, devemos em exercícios assim analisar o pior caso. Como já temos as dimensões da caixa, vamos utilizar aquela que tem o menor lado, pois a condição deve satisfazer esse lado na pior hipótese.
Sabemos que o menor lado da caixa tem 8 cm, como deve sobrar pelo menos 1 cm em cada lado, sobram então 6 cm para colocar o troféu (8 – 1 -1 = 6).
Sabemos então que escala é:
E = \frac{Tv}{Tr}Onde Tv é o tamanho virtual (miniatura) e Tr é o tamanho real.
No nosso caso Tv = 6 cm, e Tr = 50 cm.
E = \frac{6}{50}Como queremos saber o valor da altura da miniatura, utilizamos esta mesma escala para descobrir a altura X da miniatura, já que sabemos que a altura real é de 100 cm. Logo:
E = \frac{x}{100} = \frac{6}{50}Portanto, isolamos X passando o 100 multiplicando para a direita:
x = \frac{6*100}{50}Logo, resolvendo esta conta temos que:
x = 12 cm
Sabemos que a altura do troféu será de 12 cm. Mas o exercício quer saber a altura da caixa. Para isso, vale destacar que no enunciado diz que deve haver uma distância de 2 cm do troféu e da tampa da caixa, portanto somamos 2 ao valor da altura da miniatura do troféu:
x = 12 + 2 = 14 cm
Logo a altura da caixa será de 14 cm, alternativa B.
Gabarito 138 ENEM 2020: B
Confira a resolução de todos os exercícios do Enem.
Confira aqui mais resoluções no site.
Quer tirar mais de 700 em Matemática no Enem?
Conheça o e-book onde você vai aprender todas as estratégias e macetes para conseguir resolver os exercícios de matemática do Enem de uma forma:
- Muito mais organizada;
- Mais rápida;
- Economizando contas;
- Analisando os exercícios.
Adquira já o seu aqui.




