137 ENEM 2020 PPL) Pretende-se comprar uma mesa capaz de acomodar 6 pessoas, de modo que, assentadas em torno da mesa, cada pessoa disponha de, pelo menos, 60 cm de espaço livre na borda do tampo da mesa, que deverá ter a menor área possível. Na loja visitada há mesas com tampos nas formas e dimensões especificadas:
• Mesa I: hexágono regular, com lados medindo 60 cm;
• Mesa II: retângulo, com lados medindo 130 cm e 60 cm;
• Mesa III: retângulo, com lados medindo 120 cm e 60 cm;
• Mesa IV: quadrado, com lados medindo 60 cm;
• Mesa V: triângulo equilátero, com lados medindo 120 cm.
A mesa que atende aos critérios especificados é a
a) I.
b) II.
c) III.
d) IV.
e) V.
Confira abaixo a resolução completa:
Solução comentada:
O exercício quer saber “ A mesa que atende aos critérios especificados “.
Para isso vamos precisar analisar os critérios especificados pelo enunciado e apontar a mesa que atende todos os critérios.
Se liga na dica: temos claramente um exercício que envolve áreas e condições. Neste exercício vamos ter de usar várias áreas de figuras diferentes para conseguir encontrar a mesa definida pelo exercício.
Condições:
- Mesa para 6 pessoas;
- Cada pessoa tenha pelo menos 60 cm;
- Menor área possível;
Conhecendo os critérios, vamos analisar agora cada mesa para ver se atende os critérios. Ao final, aquelas que atendem os critérios vamos ter de calcular a área para escolher a que tem a menor área.
• Mesa I: hexágono regular, com lados medindo 60 cm;
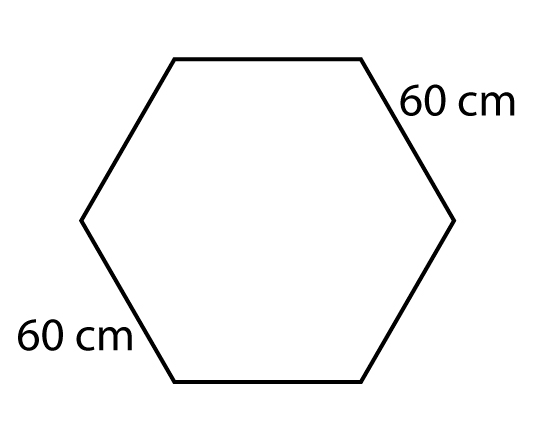
O hexágono tem 6 lados com 60 cm, logo nessa mesa cabem 6 pessoas com 60 cm. Portanto a primeira opção atende os critérios.
• Mesa II: retângulo, com lados medindo 130 cm e 60 cm;
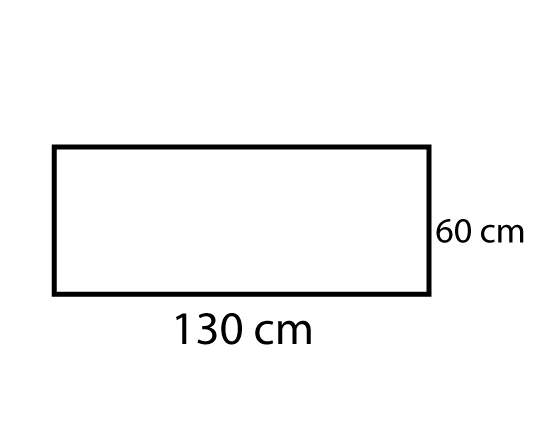
Temos dois lados com 60 cm, logo em cada lado vai duas pessoas. Nos dois outros lados tem 130 cm, sendo assim cabe duas pessoas por lado com pelo menos 60 cm. Logo esta mesa atende os critérios.
• Mesa III: retângulo, com lados medindo 120 cm e 60 cm;
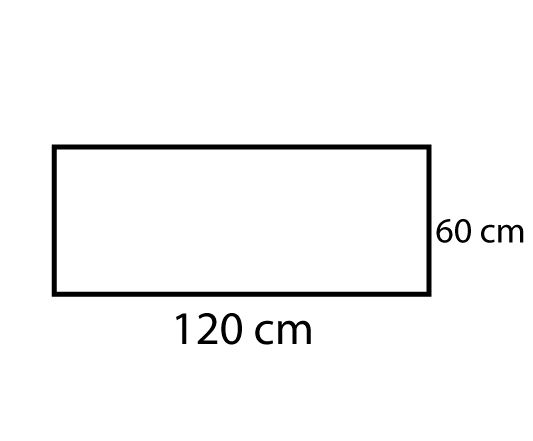
Temos dois lados com 60 cm, logo em cada lado vai duas pessoas. Nos dois outros lados temos 120 cm, sendo assim cabe duas pessoas por lado com 60 cm para cada uma. Logo esta mesa atende os critérios.
• Mesa IV: quadrado, com lados medindo 60 cm;
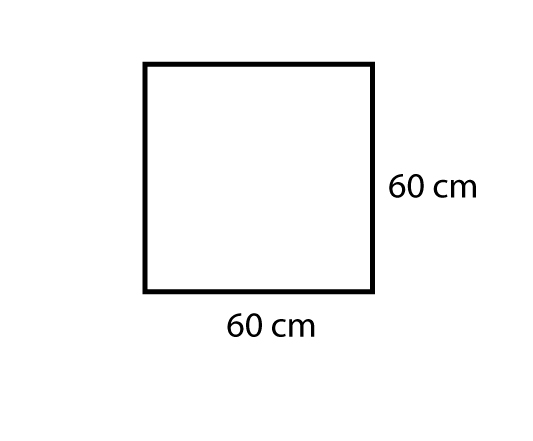
Como temos 4 lados com 60 cm, temos espaço para apenas 4 pessoas. Portanto esta mesa não atende os critérios.
• Mesa V: triângulo equilátero, com lados medindo 120 cm.
Esta mesa tem três lados com 120 cm, logo cada lado vai caber duas pessoas com pelo menos 60 cm. Sendo assim esta mesa atende os critérios.
Sendo assim, temos 4 mesas que atendem os critérios. Vamos então calcular a área dessas 4 mesas:
• Mesa I: hexágono regular, com lados medindo 60 cm;
A_I=\frac{\sqrt{3}*3}{2}*L^2=\frac{\sqrt{3}*3}{2}*60^2=5.400\sqrt{3}• Mesa II: retângulo, com lados medindo 130 cm e 60 cm;
A_{II}=130*60=7.800• Mesa III: retângulo, com lados medindo 120 cm e 60 cm;
A_{III}=120*60=7.200• Mesa V: triângulo equilátero, com lados medindo 120 cm.
A_{V}=\frac{\sqrt{3}}{4}*L^@=\frac{\sqrt{3}}{4}*120^2=3.600\sqrt{3}Entre essas três áreas podemos de cara descarta as áreas I e II. A área I é menor que a área V (ambas com raiz de 3) e área II é menor que a área III.
Comparando as áreas III e V vemos claramente que a V é menor, sabendo que raiz de 3 é aproximadamente 1,7.
Logo alternativa correta é a letra E.
Gabarito 137 ENEM 2020 PPL: E
Confira a resolução de todos os exercícios do Enem.
Confira aqui mais resoluções no site.
Quer tirar mais de 700 em Matemática no Enem?
Conheça o e-book onde você vai aprender todas as estratégias e macetes para conseguir resolver os exercícios de matemática do Enem de uma forma:
- Muito mais organizada;
- Mais rápida;
- Economizando contas;
- Analisando os exercícios.
Adquira já o seu aqui.
