157 PROVA AMARELA ENEM 2020)
Enquanto um ser está vivo, a quantidade de carbono 14 nele existente não se altera. Quando ele morre, essa quantidade vai diminuindo. Sabe-se que a meia-vida do carbono 14 é de 5 730 anos, ou seja, num fóssil de um organismo que morreu há 5 730 anos haverá metade do carbono 14 que existia quando ele estava vivo. Assim, cientistas e arqueólogos usam a seguinte fórmula para saber a idade de um fóssil encontrado: Q(t) = Q0∙2^− (t/5730) em que t é o tempo, medido em ano, Q(t) é a quantidade de carbono 14 medida no instante t e Q0 é a quantidade de carbono 14 no ser vivo correspondente.
Um grupo de arqueólogos, numa de suas expedições, encontrou 5 fósseis de espécies conhecidas e mediram a quantidade de carbono 14 neles existente. Na tabela temos esses valores juntamente com a quantidade de carbono 14 nas referidas espécies vivas.
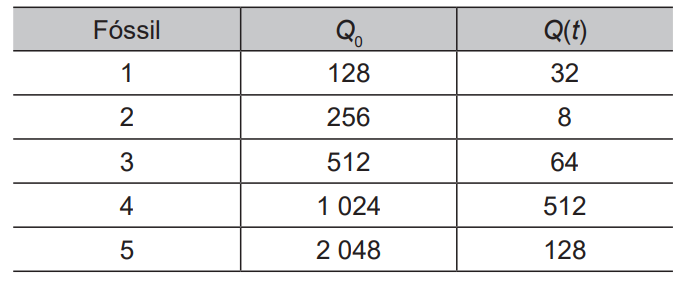
O fóssil mais antigo encontrado nessa expedição foi
A) 1.
B) 2.
C) 3.
D) 4.
E) 5.
Confira abaixo a resolução completa:
Solução comentada:
O exercício quer que seja definido o “fóssil mais antigo“. Para isso vamos ter de calcular o tempo de cada um dos 5 fósseis.
A equação dada pelo exercício para substituir os dados da tabela é:
Q(t)=Q_0*2^{-{\frac{t}{5730}}}
Para encontrar o valor de t, vamos de ter de fazer algumas operações, como passar o Q0 dividindo:
\frac{Q(t)}{Q_0}=2^{-{\frac{t}{5730}}}
Percebemos então que a relação Q(t)/Q0 deverá estar na base 2 para podermos calcular o valor de t.
Nota-se que o valor de 5730 pode ser ignorado da conta, uma vez que ele irá dividir todos os valores, portanto será uma conta desnecessária. Portanto, simplificando:
\frac{Q(t)}{Q_0}=2^{-t}\rightarrow \frac{Q(t)}{Q_0}=\frac{1}{2^t}
Logo, a divisão Q(t)/Q0 que der o o maior expoente em base 2 será o fóssil mais antigo. Resta agora só fazer as divisões:
Fóssil\ 1:\\
\frac{Q(t)}{Q_0}=\frac{1}{2^t}\ \rightarrow \frac{32}{128}=\frac{1}{2^t}\ \rightarrow \frac{1}{4}=\frac{1}{2^t} \rightarrow \frac{1}{2^2}=\frac{1}{2^t}\\
\ \\
Fóssil\ 2:\\
\frac{Q(t)}{Q_0}=\frac{1}{2^t}\ \rightarrow \frac{8}{256}=\frac{1}{2^t}\ \rightarrow \frac{1}{32}=\frac{1}{2^t} \rightarrow \frac{1}{2^5}=\frac{1}{2^t}\\
\ \\
Fóssil\ 3:\\
\frac{Q(t)}{Q_0}=\frac{1}{2^t}\ \rightarrow \frac{64}{512}=\frac{1}{2^t}\ \rightarrow \frac{1}{8}=\frac{1}{2^t} \rightarrow \frac{1}{2^3}=\frac{1}{2^t}\\
\ \\
Fóssil\ 4:\\
\frac{Q(t)}{Q_0}=\frac{1}{2^t}\ \rightarrow \frac{512}{1024}=\frac{1}{2^t}\ \rightarrow \frac{1}{2}=\frac{1}{2^t} \rightarrow \frac{1}{2^1}=\frac{1}{2^t}\\
\ \\
Fóssil\ 5:\\
\frac{Q(t)}{Q_0}=\frac{1}{2^t}\ \rightarrow \frac{128}{2048}=\frac{1}{2^t}\ \rightarrow \frac{1}{16}=\frac{1}{2^t} \rightarrow \frac{1}{2^4}=\frac{1}{2^t}\\
\ \\Logo, notando que o maior expoente é o valor 5 no fóssil 2, a alternativa correta é a letra b) fóssil 2.
Gabarito 157 ENEM 2020: B
Dica de conteúdo: Neste exercício utilizamos conceitos de funções exponenciais. Este exercício tem um grande macete que facilita muito a sua conta. Muitas pessoas demorariam mais de 15 minutos para solucionar este exercício, mas se você perceber é possível fazer esse exercício em 3 minutos tranquilamente, basta ter atenção ao processo que é utilizado ao longo da resolução comentada.
Confira a resolução de todos os exercícios do Enem.
Confira aqui mais resoluções no site.
Quer tirar mais de 700 em Matemática no Enem?
Conheça o e-book onde você vai aprender todas as estratégias e macetes para conseguir resolver os exercícios de matemática do Enem de uma forma:
- Muito mais organizada;
- Mais rápida;
- Economizando contas;
- Analisando os exercícios.
Adquira já o seu aqui.




