44 UNIOESTE 2021 – Seja a ∈ Z um número inteiro, com a ≠ 0

44 UNIOESTE 2021 :

44 UNIOESTE 2021) Seja a ∈ Z um número inteiro, com a ≠ 0 , e considere o polinômio

É CORRETO afirmar que:

A) P(x) possui apenas duas raízes reais.

B) P(x) possui três raízes reais, todas dadas em função de a.

C) a, a² e a³ são as três raízes de P(x).

D) P(x) possui uma raiz que não depende de a.

E) As três raízes de P(x) são sempre distintas, independentemente do valor de a.

Confira abaixo a resolução completa:

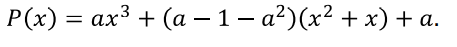
Solução comentada:

Temos claramente um exercício envolvendo funções e polinômios.

Este exercício quer informações sobre as raízes do polinômio apresentado. Sabemos que o polinômio é:

Nesse tipo de exercício o primeiro passo que você deve fazer é substituir os valores de -1 e 1 neste polinômio, para verificar se ao menos um dos dois é raiz.

Substituindo 1:

Sendo assim o valor de x=1 não é raiz.

Substituindo -1:

Como o -1 é raiz, já temos uma raiz, que é independente de a.

Para encontrar as demais podemos dividir o nosso polinômio pelo binômio x+1, que é o binômio referente a raiz -1, uma vez que (x-a) é o binômio das raízes. Sendo assim:

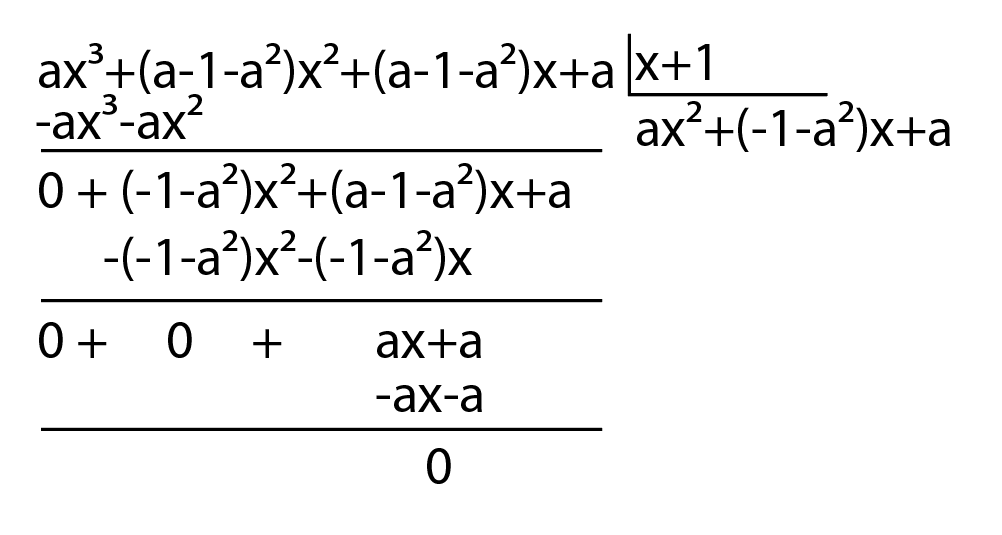
Sendo assim, sabemos que P(x) será igual a:

Logo, podemos analisar as nossas alternativas e eliminar algumas:

A) P(x) possui apenas duas raízes reais.

Ainda não sabemos, precisamos encontrar duas raízes ainda.

B) P(x) possui três raízes reais, todas dadas em função de a.

-1 não está em função de A. Logo esta está incorreta.

C) a, a² e a³ são as três raízes de P(x).

-1 é raiz do polinômio. Logo está incorreta.

D) P(x) possui uma raiz que não depende de a.

Por enquanto é verdade, mas precisamos encontrar as outras duas.

E) As três raízes de P(x) são sempre distintas, independentemente do valor de a.

Duas raízes vão depender de a, devido a nossa função. Portanto está incorreta.

Portanto, para encontrar qual a alternativa correta entre A e D, vamos precisar encontrar as outras duas raízes.

Para isso vamos calcular as raízes referentes ao polinômio de segundo grau, da segunda parte do polinômio geral:

Para saber se as raízes serão reais o valor de delta não pode ser negativo. Sendo assim, vamos estudar seu sinal, calculando o Delta desta expressão:

Logo, como esse Delta é zero, a nossa função nunca será negativa.

Sendo assim todas as raízes serão reais.

Logo a alternativa correta é a letra D.

GABARITO 44 UNIOESTE 2021 : D.

Confira a resolução de todos os exercícios do Unioeste.

Confira aqui mais resoluções no site.

Quer tirar mais de 700 em Matemática no Enem?

Conheça o e-book onde você vai aprender todas as estratégias e macetes para conseguir resolver os exercícios de matemática do Enem de uma forma:

• Muito mais organizada;
• Mais rápida;
• Economizando contas;
• Analisando os exercícios.

Adquira já o seu aqui.