43 UNIOESTE 2021 – Considere uma função bijetora f: (a, b) -> R e

43 UNIOESTE 2021 :

43 UNIOESTE 2021) Considere uma função bijetora f: (a, b) -> R e sua inversa f^-1: R-> (a, b).

Suponha ainda que

para todo (x, y) ∈ (a, b), com x+y ∈ (a, b).

Se x, y e z são números reais que satisfazem a igualdade

então é CORRETO afirmar que x, y e z satisfazem:

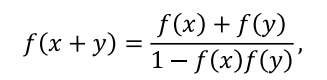
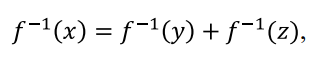
A) x = y + z.

B) yz = xy + xz.

C) xyz = x – y – z.

D) y + z – x = a.

E) x- y – z = b.

Confira abaixo a resolução completa:

Solução comentada:

Temos claramente um exercício envolvendo funções.

O comando do exercício é: então é CORRETO afirmar que x, y e z satisfazem.

Logo, queremos encontrar uma relação entre x, y e z. Para encontrar essa relação é simples: vamos necessitar pegar a relação das funções inversas e aplicar as propriedades apresentadas para conseguir solucionar.

Temos que a relação entre as funções inversas é:

f^{-1}(x)=f^{-1}(y)+f^{-1}(z)

Logo, para conseguirmos relacionar x, y e z, vamos aplicar a função f nessas funções inversas, lembrando que por propriedade de funções:

f(f^{-1}(a))=a

Sendo assim aplicando a função f dos dois lados:

f(f^{-1}(x))=f(f^{-1}(y)+f^{-1}(z))

Para o lado esquerdo o resultado será x. Já para o lado direito, como temos uma soma dentro da função vamos aplicar a propriedade dada no enunciado:

x=\frac{f(f^{-1}(y))+f(f^{-1}(z))}{1-f(f^{-1}(y))f(f^{-1}(z))}\\
\ \\
x=\frac{y+z}{1-yz}\\
\ \\
x(1-yz)=y+z\\
\ \\
x-xyz=y+z\\
\ \\
x-y-z=xyz\\
\ \\

Logo a alternativa que nos trás esta resposta é a alternativa C.

GABARITO 43 UNIOESTE 2021 : C.

Confira a resolução de todos os exercícios do Unioeste.

Confira aqui mais resoluções no site.

Quer tirar mais de 700 em Matemática no Enem?

Conheça o e-book onde você vai aprender todas as estratégias e macetes para conseguir resolver os exercícios de matemática do Enem de uma forma:

• Muito mais organizada;
• Mais rápida;
• Economizando contas;
• Analisando os exercícios.

Adquira já o seu aqui.