33 UEPG 2021 – Sabendo que o piso de uma academia tem a forma

33 UEPG 2021:

33 UEPG 2021) Sabendo que o piso de uma academia tem a forma deum trapézio isósceles com P metros de perímetro e cujos lados paralelos medem 60 metros e 30 metros, assinale o que for correto.

01) Se P = 140 metros, então a área do trapézio mede 900 m².

02) A altura do trapézio, em função de P, é dado pela relação

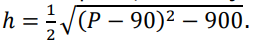
04) Se P = 160 metros, então a altura do trapézio é maior que 30 metros.
08) Se a altura do trapézio mede 20 metros, então P = 140 metros.

Confira abaixo a resolução completa:

Solução comentada:

Temos claramente um exercício envolvendo geometria plana.

O piso da academia é um trapézio isóceles isto é, com os dois lados não paralelos iguais, como podemos ver na imagem abaixo.

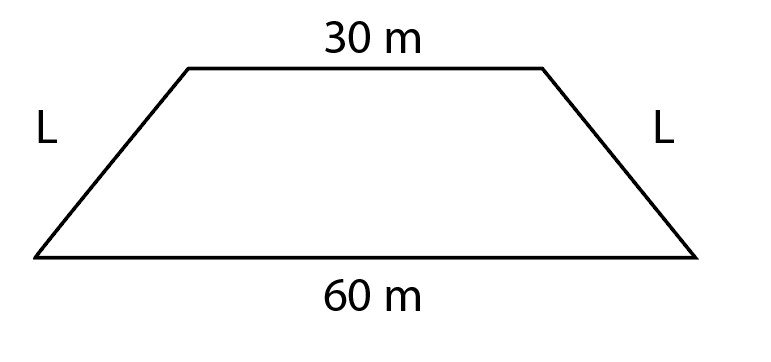
Vamos agora para as sentenças.

01) Se P = 140 metros, então a área do trapézio mede 900 m².

Sabendo que P vale 140, primeiro precisamos identificar quem é L para conseguir encontrar o valor da altura do trapézio através de pitágoras:

2L+30+60=P\\
\ \\
2L+90=140\\
\ \\
2L=140-90\\
\ \\
L=\frac{50}{2}=25

Sabendo que L é igual a 25 conseguimos encontrar a altura:

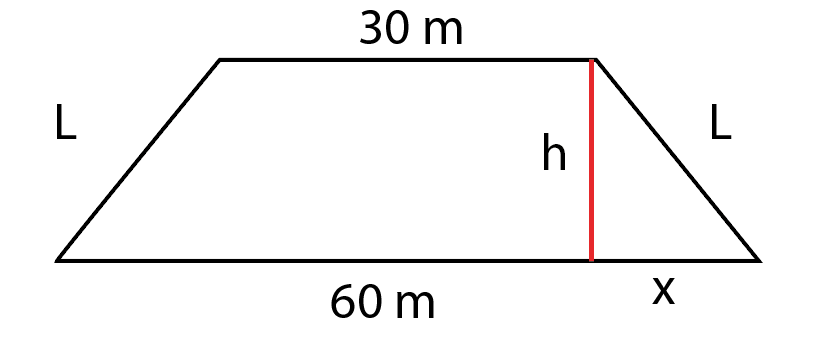
Antes de encontrar a altura, sabendo que L=25, precisamos encontrar quem é x.

Sabemos que a x será metade da diferença de 60 para 30. Logo, podemos dizer que x=15.

Sendo assim, por meio de pitágoras conseguimos encontrar o valor de h:

h^2+15^2=25^2\\
\ \\
h^2=625-225\\
\ \\
h=\sqrt{400}=20

Como a altura mede 20, conseguimos calcular a área do trapézio:

A_T=\frac{(B+b)h}{2}=\frac{(60+30)20}{2}=900

Logo, a 01 está correta.

02) A altura do trapézio, em função de P, é dado pela relação

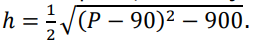
Para encontrar o valor de h sem saber L, podemos fazer da seguinte forma, encontrando primeiro L em função de P:

2L+90=P\\
\ \\
2L=P-90\\
\ \\
L=\frac{P-90}{2}

L^2=h^2+15^2\\
\ \\
L^2-225=h^2\\
\ \\
\sqrt{L^2-225}=h\\
\ \\
Substituindo\ L:\\
\ \\
\sqrt{(\frac{P-90}{2})^2-225}=h\\
\ \\
\sqrt{\frac{1}{4}(P-90)^2-225}=h\\

Para não ter fração dentro da raiz podemos tirar o 1/4 pra fora da raiz, sabendo que raiz de 1/4 é 1/2. Mas para isso precisamos multiplicar o 225 por 4:

\sqrt{\frac{1}{4}(P-90)^2-225}=h\\
\ \\
\frac{1}{2}\sqrt{(P-90)^2-4*225}=h\\
\ \\
\frac{1}{2}\sqrt{(P-90)^2-900}=h\\

Justamente o que a sentença 02 nos trás. Sendo assim a 02 é a alternativa correta.

04) Se P = 160 metros, então a altura do trapézio é maior que 30 metros.

Basta substituir P na equação que acabamos de encontrar:

\frac{1}{2}\sqrt{(P-90)^2-900}=h\\
\ \\
\frac{1}{2}\sqrt{(160-90)^2-900}=h\\
\ \\
\frac{1}{2}\sqrt{4900-900}=h\\
\ \\
\frac{1}{2}\sqrt{4000}=h\\
\ \\
\frac{20}{2}\sqrt{10}=h\\
\ \\
10\sqrt{10}=h\\

Como sabemos que raiz de 10 é maior que 3, sabemos que a altura será maior que 3, logo 10 multiplicado por um número maior que 3 podemos dizer que é maior que 30. Sendo assim a 04 é a alternativa correta.

08) Se a altura do trapézio mede 20 metros, então P = 140 metros.

A sentença 04 é comprovada na sentença 01, onde encontramos h=20. Logo a sentença 08 está correta.

Logo, como todas estão corretas, o somatório é: 1+2+4+8=15

GABARITO 33 UEPG 2021: 15.

Confira a resolução de todos os exercícios do Enem.

Confira aqui mais resoluções no site.

Quer tirar mais de 700 em Matemática no Enem?

Conheça o e-book onde você vai aprender todas as estratégias e macetes para conseguir resolver os exercícios de matemática do Enem de uma forma:

• Muito mais organizada;
• Mais rápida;
• Economizando contas;
• Analisando os exercícios.

Adquira já o seu aqui.