01. O número de anagramas da palavra VITÓRIA que começam e terminam com consoante é
360.
02. Com os algarismos 1, 2, 3, 7 e 8 são formados números de cinco algarismos distintos. Se
listássemos, em ordem decrescente, todos os números obtidos, então a posição do número
27.813 seria a 80a.
04. O termo independente no desenvolvimento de (x+1/x)^6 é um divisor de 5.
08. Um grupo de 75 pessoas foi entrevistado sobre doenças. Foi constatado entre os entrevistados que 16 pessoas já tiveram as doenças A, B e C; 30 já tiveram as doenças A e C; 24 já tiveram as doenças A e B; 22 já tiveram as doenças B e C; 6 tiveram apenas a doença A; 9 tiveram apenas a doença B; e 5 tiveram apenas a doença C. Se escolhermos ao acaso um dos entrevistados, a probabilidade de essa pessoa não ter sido acometida com nenhuma das três doenças é maior do que 20%.
16. Um grupo de 12 torcedores, sendo 8 do time A e os demais do time B, participou de um sorteio para assistir a um importante jogo do campeonato. Ficou estabelecido que fossem escolhidos 9 torcedores para essa ocasião. Se, entre os 9 escolhidos, 6 devem ser torcedores de A e 3 devem ser torcedores de B, então existem 112 formas distintas de escolher esses torcedores.
Confira abaixo a resolução completa:
Solução comentada:
01. O número de anagramas da palavra VITÓRIA que começam e terminam com consoante é 360.
Este exercício é um exercício de análise combinatória. Temos que calcular os anagramas da palavra vitória que começam e terminam com consoante. Sendo assim, temos que são 7 tracinhos, logo:
\_\_\ \_\_ \ \_\_ \ \_\_\ \_\_ \ \_\_\ \_\_
Para o primeiro tracinho, como temos 3 consoantes, vamos ter o número 3. Para o último, como uma consoante já foi utilizada no primeiro, vamos ter duas:
\underline{\ 3\ }\ \_\_ \ \_\_ \ \_\_\ \_\_ \ \_\_\ \underline{\ 2\ }Para os demais, serão as 5 letras que sobram em fatorial:
\underline{\ 3\ }\ \underline{\ 5\ } \ \underline{\ 4\ } \ \underline{\ 3\ } \ \underline{\ 2\ } \ \underline{\ 1\ } \ \underline{\ 2\ } =720Esse resultado temos que dividir por 2!, uma vez que temos duas letras i, sendo assim:
\frac{720}{2!}=360Como o número de possibilidades é 360, a sentença 01 está correta.
02. O 02. Com os algarismos 1, 2, 3, 7 e 8 são formados números de cinco algarismos distintos. Se
listássemos, em ordem decrescente, todos os números obtidos, então a posição do número
27.813 seria a 80a.
O exercício quer saber qual a posição do número 27.813, em ordem decrescente. Sendo assim, vamos calcular quantos números a gente consegue formar com cada número sendo iniciado.
Como é em ordem decrescente, vamos começar com o 8 fixado, contabilizando as possibilidades nas demais posições:
\underline{\ |8|\ }\ \underline{\ 4\ } \ \underline{\ 3\ } \ \underline{\ 2\ } \ \underline{\ 1\ } \ =24Temos então 24 possibilidades começando com o 28.
O próximo número em ordem decrescente é o 4 e logo após o 3, sendo assim:
\underline{\ |4|\ }\ \underline{\ 4\ } \ \underline{\ 3\ } \ \underline{\ 2\ } \ \underline{\ 1\ } \ =24\\
\ \\
\underline{\ |3|\ }\ \underline{\ 4\ } \ \underline{\ 3\ } \ \underline{\ 2\ } \ \underline{\ 1\ } \ =24\\
\ \\
Sendo\ assim\ até\ o\ momento\ temos:\\
\ \\
24+24+24=72\ possibilidadesAgora, entrando no algarismo 2 como início, temos que vamos começar com o 2, e na segunda posição vamos fixar o 8, para ser em ordem decrescente novamente:
\underline{\ |2|\ }\ \underline{\ |8|\ } \ \underline{\ 3\ } \ \underline{\ 2\ } \ \underline{\ 1\ } \ =6Temos então 6 possibilidades, somando com 72 anteriores são 78 possibilidades.
Sendo assim, vamos ver as próximas em ordem decrescente:
\underline{\ |2|\ }\ \underline{\ |7|\ } \ \underline{\ |8|\ } \ \underline{\ |3|\ } \ \underline{\ |1|\ } \ - 79º\\
\ \\
\underline{\ |2|\ }\ \underline{\ |7|\ } \ \underline{\ |8|\ } \ \underline{\ |1|\ } \ \underline{\ |3|\ } \ - 80ºLogo, realmente, o número 27.813 ocupa a posição 80. Portanto, a sentença 02 está correta.
04. O termo independente no desenvolvimento de (x+1/x)^6 é um divisor de 5.
Queremos saber qual é o termo independente deste binômio. Para isso, utilizamos a seguinte expressão:
T_{p+1}=C_n^p*x^{n-2p}\\
\ \\
Sabemos que n é o expoente do binômio, portanto n=6.
Para termos um termo independente, o expoente de x tem que ser igual a zero, logo:
n-2p=0\\
\ \\
6-2p=0\\
\ \\
6=2p\\
\ \\
\frac{6}{2}=p\\
\ \\
3=pComo p=3, temos que:
T_{p+1}=C_n^p*x^{n-2p}\\
\ \\
T_{4}=C_6^3*x^{6-2*3}\\
\ \\
T_{4}=C_6^3*x^{0}\\
\ \\
T_{4}=C_6^3=\frac{6!}{3!*3!}=20\\
\ \\Logo, o termo independente vale 20, este valor não é divisor de 5, mas sim pode ser dividido por 5. Sendo assim, a sentença 04 está incorreta.
08. Um grupo de 75 pessoas foi entrevistado sobre doenças. Foi constatado entre os entrevistados que 16 pessoas já tiveram as doenças A, B e C; 30 já tiveram as doenças A e C; 24 já tiveram as doenças A e B; 22 já tiveram as doenças B e C; 6 tiveram apenas a doença A; 9 tiveram apenas a doença B; e 5 tiveram apenas a doença C. Se escolhermos ao acaso um dos entrevistados, a probabilidade de essa pessoa não ter sido acometida com nenhuma das três doenças é maior do que 20%.
Logo, temos um exercício de conjuntos. Vamos utilizar de um Diagrama de Venn para solucionar este exercício e encontrar a probabilidade de essa pessoa não ter sido acometida por nenhuma doença.
Primeiramente, temos 3 doenças, logo vamos ter 4 círculos: doença A, doença B, doença C e nenhuma doença:
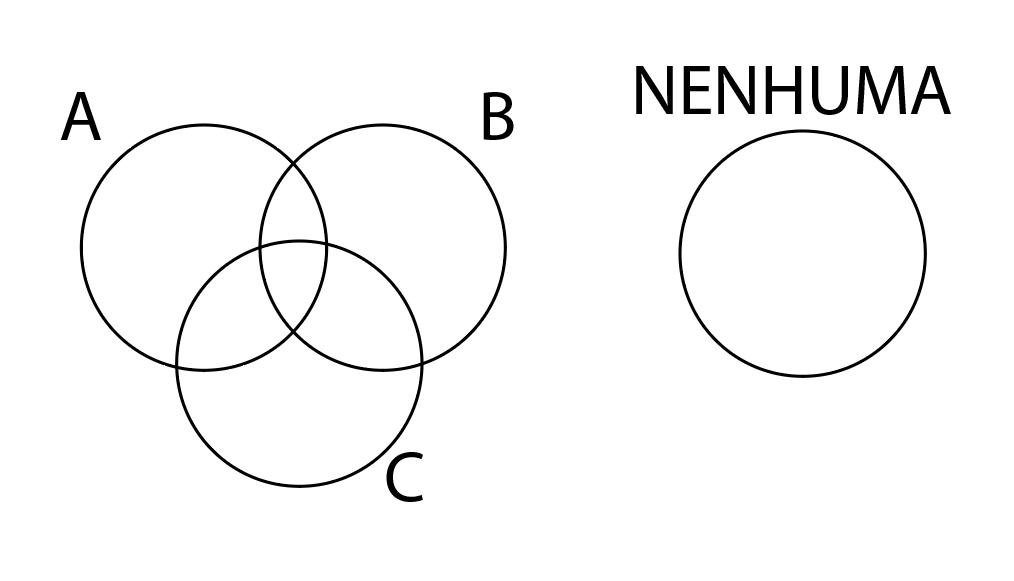
16 pessoas já tiverem as doenças A,B e C, logo:
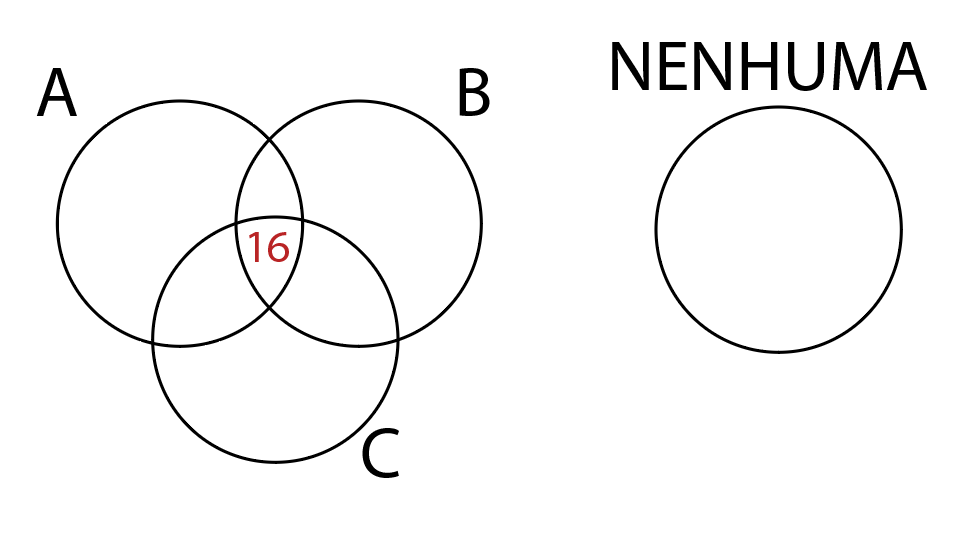
30 já tiveram as doenças A e C, mas dessas 30 temos que descontar 16 que já estão no diagrama, ficando 30-16=14.
24 já tiveram as doenças A e B, mas dessas 24 temos que descontar 16 que já estão no diagrama, ficando 24-16=8
22 já tiveram as doenças B e C, mas dessas 22 temos que descontar 16 que já estão no diagrama, ficando 22-16=6
Sendo assim:
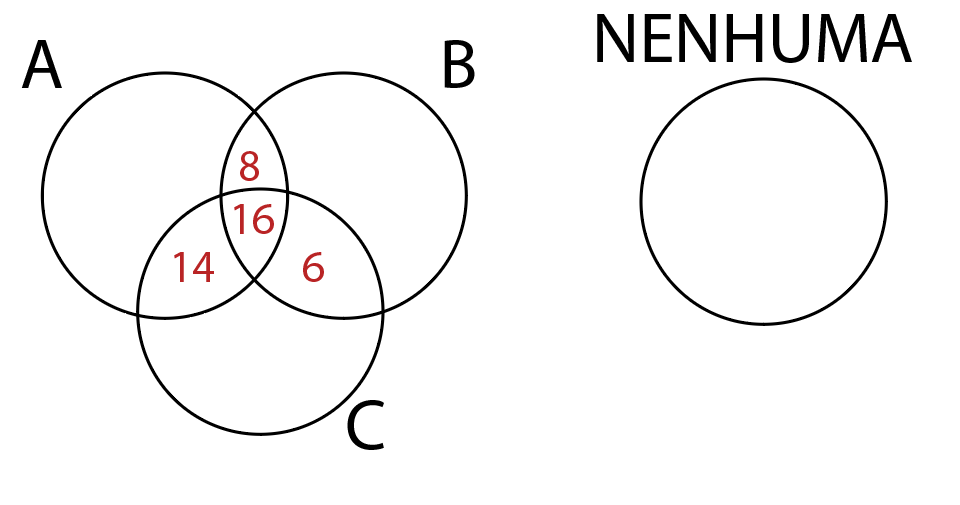
6 tiveram apenas a doença A, 9 tiveram apenas a doença B e 5 tiveram apenas a doença C. Sendo assim:
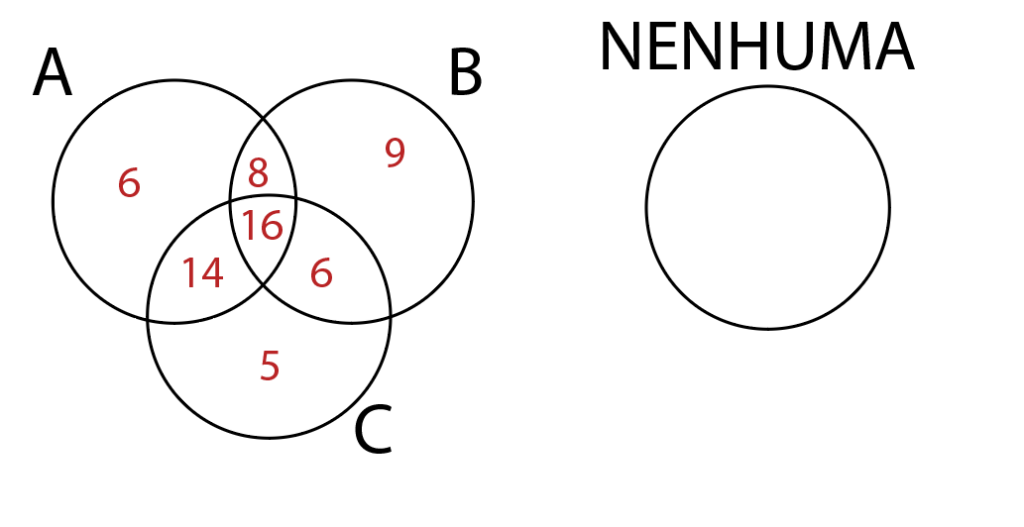
Como eram 75 pessoas no total, podemos então calcular quantas pessoas não tiveram nenhuma doença, fazendo:
75-6-8-9-14-16-6-5=11
Como são 11 pessoas:
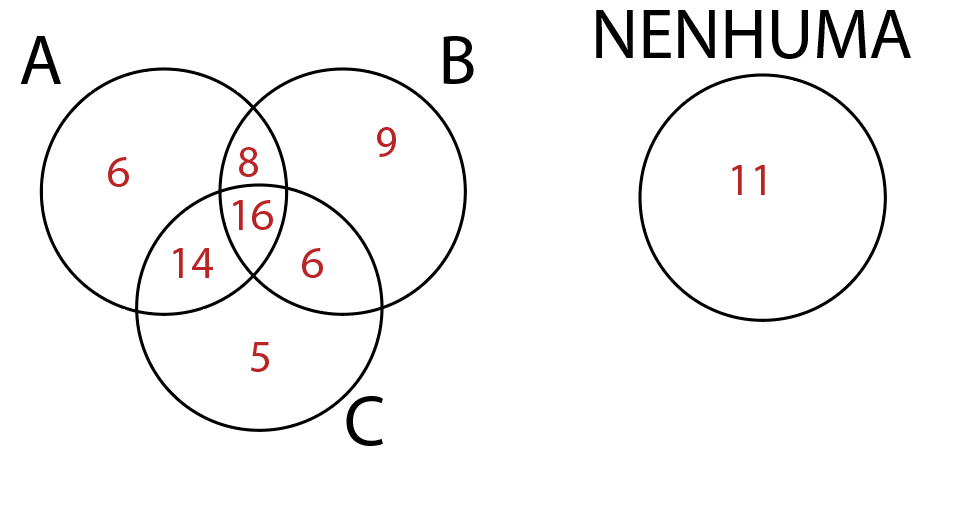
Logo, a probabilidade será dada pelo número de pessoas que não teve nenhuma doença dividida pelo número total de pessoas:
P=\frac{11}{75}\approx0,14\approx14%Como é aproximadamente 14% não é maior que 20%. Sendo assim a sentença 08 está incorreta.
16. Um grupo de 12 torcedores, sendo 8 do time A e os demais do time B, participou de um sorteio para assistir a um importante jogo do campeonato. Ficou estabelecido que fossem escolhidos 9 torcedores para essa ocasião. Se, entre os 9 escolhidos, 6 devem ser torcedores de A e 3 devem ser torcedores de B, então existem 112 formas distintas de escolher esses torcedores.
O exercício quer saber de quantas formas diferentes podemos escolher esses torcedores, sabendo que:
- 8 torcedores de A;
- 4 torcedores de B;
- serão escolhidos 9 torcedores;
- 6 serão de A;
- 3 serão de B;
Logo, vamos ter de calcular a quantidade de formas diferentes que podemos escolher os torcedores de A e os torcedores de B, e depois multiplicar, uma vez que são torcedores de A e torcedores de B.
A quantidade de formas diferentes será dada por uma combinação. Uma vez que se você escolher TORCEDOR 1 e TORCEDOR 2 é a mesma coisa que TORCEDOR 2 e TORCEDOR 1, logo a ordem não interfere. Sendo assim:
Para os torcedores do time A será uma combinação de 8 torcedores escolhidos 6 a 6.
Para os torcedores do time B será uma combinação de 4 torcedores escolhidos 3 a 3.
C_8^6*C_4^3=\frac{8!}{6!*2!}*\frac{4!}{3!*1!}=\frac{8*7}{2*1}*\frac{4}{1}=4*7*4=112Como o número de possibilidades realmente é 112, a sentença 32 está correta.
GABARITO 22 UFSC 2020: 19.
Confira a resolução de todos os exercícios do Enem.
Confira aqui mais resoluções no site.
Quer tirar mais de 700 em Matemática no Enem?
Conheça o e-book onde você vai aprender todas as estratégias e macetes para conseguir resolver os exercícios de matemática do Enem de uma forma:
- Muito mais organizada;
- Mais rápida;
- Economizando contas;
- Analisando os exercícios.
Adquira já o seu aqui.




