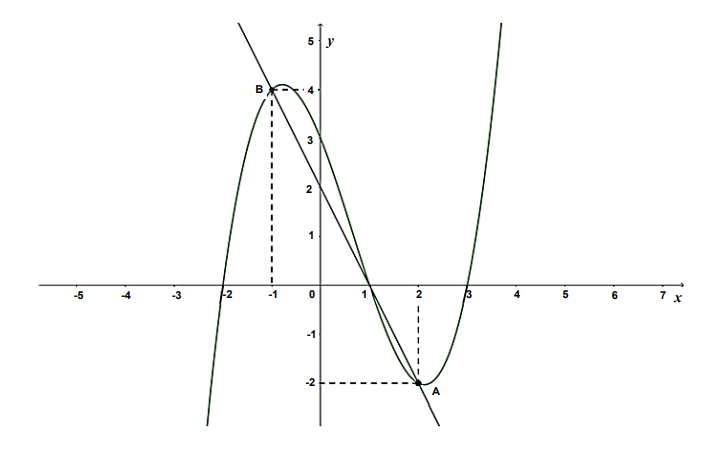
01. o polinômio 𝑝 pode ser expresso por 𝑝(𝑥) = (𝑥 + 2)(𝑥 − 1)(𝑥 − 3)
02. o resto da divisão do polinômio 𝑝 por 𝑥²/4 − 𝑥 + 3/4 é zero.
04. o polinômio ℎ pode ser expresso por ℎ(𝑥) = −𝑥 + 2.
08. se o resultado da soma 𝑝(𝑥) + ℎ(𝑥) é 𝑞(𝑥), então o polinômio 𝑞 tem grau 3 e seu termo
independente é 5.
16. 𝑝(−3) = −12.
32. o polinômio 𝑝 é crescente para 𝑥 ∈ (−∞, −1)𝑈(1, +∞).
64. a área do triângulo que possui como vértices os pontos 𝐴, 𝐵 e a origem do sistema de
coordenadas cartesianas é igual a 3 unidades de área.
Confira abaixo a resolução completa:
Solução comentada:
01. o polinômio 𝑝 pode ser expresso por 𝑝(𝑥) = (𝑥 + 2)(𝑥 − 1)(𝑥 − 3)
Para sabermos se isso é verdade vamos substituir um dos pontos, A ou B, dentro dessa expressão. Se o valor da imagem estiver correto para ambos então realmente é esta expressão.
Substituindo o ponto B(-1,4):
p(-1)=(-1+2)(-1-1)(-1-3)=(1)(-2)(-4)=8
Como 8 é diferente de 4 temos que esta expressão não representa corretamente o polinômio p(x).
Sendo assim a 01 está incorreta.
02. o resto da divisão do polinômio 𝑝 por 𝑥²/4 − 𝑥 + 3/4 é zero.
Para dividirmos p(x) por esta expressão temos primeiramente definir quem é p(x).
Sabemos que a expressão da 01 está parcialmente correta, uma vez que ela representa de maneira correta as 3 raízes da função p(x). O que falta para aquele polinômio é identificar quem é o a, uma vez que:
p(x) = a(x+2)(x-1)(x-3).
Como o valor que resultou da conta anterior foi 8, e era para ser 4. Podemos identificar que o valor de a é 1/2, para resultar em 4. Sendo assim, p(x) é:
p(x) = 1/2(x+2)(x-1)(x-3).
Logo, podemos trabalhar essa função para poder dividi-lá, sendo assim multiplicando os dois primeiros binômios e depois desenvolvendo:
p(x)=\frac{1}{2}*(x^2+x-2)(x-3)\\
\ \\
p(x)=\frac{1}{2}*(x^3-2x^2-5x+6)\\
Tendo o polinômio p(x), podemos utilizar um polinômio p'(x) multiplicado por 2 para poder fazer a divisão:
p'(x)=2*p(x)=(x^3-2x^2-5x+6)\\
Para o polinômio da divisão faremos o mesmo, desta vez multiplicando todos os elementos por 4:
(\frac{x^2}{4}-x+\frac{3}{4})*4\\
\ \\
x^2-4x+3Tendo os polinômios, agora podemos fazer a divisão:
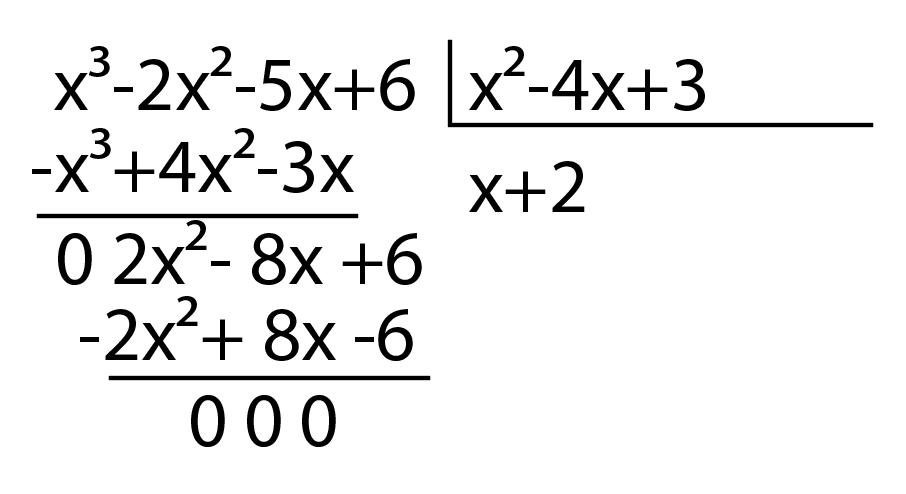
Sendo assim, podemos observar que o resto realmente é zero, logo a sentença 02 está correta.
04. o polinômio ℎ pode ser expresso por ℎ(𝑥) = −𝑥 + 2.
Para verificar se essa expressão é verdadeira é simples, basta substituir o ponto A e o ponto B nesta função, se um deles der errado essa expressão é inválida.
Vamos substituir o ponto B(2,-2):
h(2)=-2+2=0
Como deveria resultar em -2 e resultou em 0, a sentença 04 está incorreta.
08. se o resultado da soma 𝑝(𝑥) + ℎ(𝑥) é 𝑞(𝑥), então o polinômio 𝑞 tem grau 3 e seu termo independente é 5.
Para sabermos qual será o termo independente de q(x), basta primeiramente identificarmos qual é o polinômio h(x).
Para isso sabemos que 1 é a raiz da função, podemos substituir:
0=a*1+b\\ a=-b\\
Usando o ponto B(2,-2) podemos encontrar mais uma equação:
-2=a*2+b\\ \ \\ -2=2a+b\\ \ \\ Como\ a=-b\ substituindo:\\ \ \\ -2=2a-a\\ \ \\ -2=a\\ \ \\ Logo, b\ vale:\\ \ \\ b=2\\ \ \\ Sendo\ assim: \\ \ \\ h(x) = -2x+2
Sabemos que o termo independente de h(x) vale 2, agora só precisamos identificar o termo independente de p(x):
p(x)=\frac{1}{2}*(x^3-2x^2-5x+6)\\
\ \\
p(x)=\frac{x^3}{2}-\frac{2x^2}{2}-\frac{5x}{2}+\frac{6}{2}\\
\ \\
p(x)=\frac{x^3}{2}-x^2-\frac{5x}{2}+3Logo, o termo independente de p(x) é 3, sendo assim somando ambos temos que:
3+2=5
Como o valor é 5, realmente a sentença 08 está correta.
16. 𝑝(−3) = −12.
Basta substituir -3 em x na função p(x):
p(x)=\frac{x^3}{2}-x^2-\frac{5x}{2}+3\\
\ \\
p(-3)=\frac{(-3)^3}{2}-(-3)^2-\frac{5(-3)}{2}+3\\
\ \\
p(-3)=\frac{-27}{2}-9-\frac{-15}{2}+3\\
\ \\
p(-3)=-12\\Logo, como p(-3)= -12, então a sentença 16 está correta.
32. o polinômio 𝑝 é crescente para 𝑥 ∈ (−∞, −1)𝑈(1, +∞)
Sentença 32 está incorreta. Pois de 1 até 2 a função é decrescente.
64. a área do triângulo que possui como vértices os pontos 𝐴, 𝐵 e a origem do sistema de coordenadas cartesianas é igual a 3 unidades de área.
Para solucionar este problema e encontrar a área podemos encontrar através da seguinte expressão:
A_\Delta=\frac{1}{2}|D|Onde |D| é o módulo do determinante da matriz D formada pelos pontos das extremidades do triângulo, sendo assim, definindo a matriz:
\begin{bmatrix}
2 & -2 & 1\\
0 & 0 & 1\\
-1 & 4 & 1
\end{bmatrix}\\
\ \\
Calculando\ o\ determinante:\\
\ \\
2-(8)=-6Substituindo na equação para encontrar a área:
A_\Delta=\frac{1}{2}|-6|\\
\ \\
A_\Delta=\frac{1}{2}*6\\
\ \\
A_\Delta=3Sendo assim, a sentença 64 está correta.
GABARITO 21 UFSC 2020: 90.
Confira a resolução de todos os exercícios do Enem.
Confira aqui mais resoluções no site.
Quer tirar mais de 700 em Matemática no Enem?
Conheça o e-book onde você vai aprender todas as estratégias e macetes para conseguir resolver os exercícios de matemática do Enem de uma forma:
- Muito mais organizada;
- Mais rápida;
- Economizando contas;
- Analisando os exercícios.
Adquira já o seu aqui.




